明日の設計図
たまにロボットを考えるブログ・・・。
[PR]
×
[PR]上記の広告は3ヶ月以上新規記事投稿のないブログに表示されています。新しい記事を書く事で広告が消えます。
4自由度ヘビの軌道生成?③
軌道上を通った場合の関節角度の決定方法は前回の通りです。
で軌道を決定する上での残ったパラメータは
●Sinの周期の長さ
●振幅
●↑とロボットのサイズ比
です。
こんかいは
2π:1:???
で???のところを、0.5,0.75,1.5(ロボットの3節を1:2:1とする)
というのを試しました。
で、ベターだったのは1.5です。
・・・ちなみに0.75では推進できませんでした。床にごむしーとを敷くと推進できましたが・・・つまり、摩擦が充分であればもっといい感じになるのでしょう。・・・広大なごむしーと・・・ほしぃ。
生成した軌道は
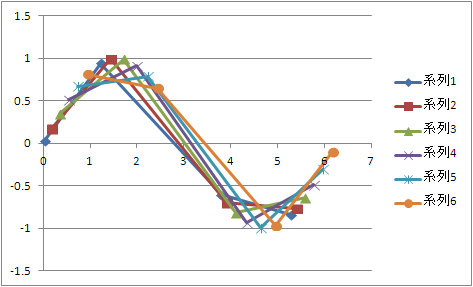
こんな軌道ととおり、
角度としては
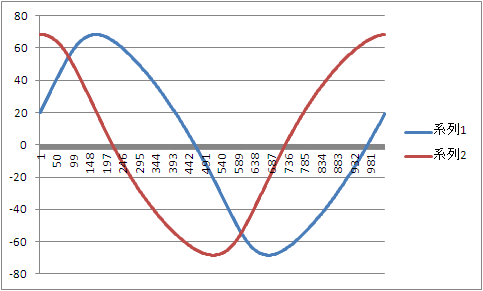
こんな感じになります。
後ろの関節と、前の関節の軌道は違うものでした。
「どっちが前?」というのは綺麗に分かれるようです。
実機の動作は
このようになり、前後というのははっきりしています。
動画からは、
・推進出来る時、出来ない時
・想定した軌道とのズレ
が明確に分かります。
なので、なるべく「推進できる時」というのを1周期ないで多く確保する軌道
というのを推定できると思いますが・・・
ま、あ、そろそろ飽きた・・・か・・・な。
で軌道を決定する上での残ったパラメータは
●Sinの周期の長さ
●振幅
●↑とロボットのサイズ比
です。
こんかいは
2π:1:???
で???のところを、0.5,0.75,1.5(ロボットの3節を1:2:1とする)
というのを試しました。
で、ベターだったのは1.5です。
・・・ちなみに0.75では推進できませんでした。床にごむしーとを敷くと推進できましたが・・・つまり、摩擦が充分であればもっといい感じになるのでしょう。・・・広大なごむしーと・・・ほしぃ。
生成した軌道は
こんな軌道ととおり、
角度としては
こんな感じになります。
後ろの関節と、前の関節の軌道は違うものでした。
「どっちが前?」というのは綺麗に分かれるようです。
実機の動作は
このようになり、前後というのははっきりしています。
動画からは、
・推進出来る時、出来ない時
・想定した軌道とのズレ
が明確に分かります。
なので、なるべく「推進できる時」というのを1周期ないで多く確保する軌道
というのを推定できると思いますが・・・
ま、あ、そろそろ飽きた・・・か・・・な。
PR
4自由度ヘビの軌道生成?①
くねくね移動がうまくいかないので、
上手くいくくねくね軌道を幾何学的に決定します。
偉い人から
「蛇行軌道にすべての車輪がのっかっていて、接線の方向を向いているべき」
とのお話を頂きましたので、それを検討します。
①sin関数にのっかる
②車輪が軌道にのるように角度を決定する
③もうひとつの車輪も同様に角度を決定する
だと思いましたが!
良く考えると・・・
平面的には2自由度、3節あります。
1個目の車輪は、のせられます。
2個目は?
1個目の車輪の位置と姿勢、例えば、
x=0,y=0,θ=45°
とかだとします。
すると、1個目の関節の位置は
x=cos45,y=sin45
です。
そこから1つめのモータの角度を変えて、
2個目の車輪を軌道に乗るように決めます。
すると、角度は接線方向になりません?!
困りました。
モータ1個では、位置&角度を決めるのは無理で、どちらか一方しか決められません。
困りました。
でもまあ、仕方ないので、接線は諦めることにしまして
各関節が、軌道に乗るような角度を決めていこうと思います。
と思いましたが、これも意外と大変。
3節あるヘビロボットの1節目のリンクだけを考えます。
このリンクの両端点がsin関数上に乗ってくれればいいのですが・・・
どうやって載せるんでしょう?
リンクを直線だと思って、x軸からの傾きを決める他ありません。
これはつまり、中心がsin関数上の円とsin関数の交点を求める問題です。

が、そのとき方については僕は収束計算以外の方法を知りません。
例えば
y=0,x=0からx=x,y=sinx
までの距離は、平方根の中に三角関数の2乗があるというこれまた難しい。
で、
その距離=リンクの長さ
という方程式を解く必要があるわけですが、
sqrt ( x*x + sinx*sinx ) = リンク長さ
うんむずかしい
。。。
プログラムを書く感じです。
・sin関数1周期を移動量、振幅を移動量にして、m単位でロボットの実現できるサイズで用意します。それを軌道関数(x)にします。
・xを入れます。→軌道関数(x)がもとまります。
・始点を決めます。
・始点からxを少し増やして、軌道関数を求めます。で距離を求めます。
・・・上を距離がいい具合になるまでやります。そのときのxをx1として覚えます。
・x1からすこしずつxを増やし、またちょうどいい距離までやってそれをx2とします。
・同様の方法でx3を決定します。
・・・これで、一番最初のヘビの形が決まりました。
・これを軌道関数1周期分計算します。
・データテーブルとして保存します。
・mbedに入れます。
これで動くんじゃね。
上手くいくくねくね軌道を幾何学的に決定します。
偉い人から
「蛇行軌道にすべての車輪がのっかっていて、接線の方向を向いているべき」
とのお話を頂きましたので、それを検討します。
①sin関数にのっかる
②車輪が軌道にのるように角度を決定する
③もうひとつの車輪も同様に角度を決定する
だと思いましたが!
良く考えると・・・
平面的には2自由度、3節あります。
1個目の車輪は、のせられます。
2個目は?
1個目の車輪の位置と姿勢、例えば、
x=0,y=0,θ=45°
とかだとします。
すると、1個目の関節の位置は
x=cos45,y=sin45
です。
そこから1つめのモータの角度を変えて、
2個目の車輪を軌道に乗るように決めます。
すると、角度は接線方向になりません?!
困りました。
モータ1個では、位置&角度を決めるのは無理で、どちらか一方しか決められません。
困りました。
でもまあ、仕方ないので、接線は諦めることにしまして
各関節が、軌道に乗るような角度を決めていこうと思います。
と思いましたが、これも意外と大変。
3節あるヘビロボットの1節目のリンクだけを考えます。
このリンクの両端点がsin関数上に乗ってくれればいいのですが・・・
どうやって載せるんでしょう?
リンクを直線だと思って、x軸からの傾きを決める他ありません。
これはつまり、中心がsin関数上の円とsin関数の交点を求める問題です。
が、そのとき方については僕は収束計算以外の方法を知りません。
例えば
y=0,x=0からx=x,y=sinx
までの距離は、平方根の中に三角関数の2乗があるというこれまた難しい。
で、
その距離=リンクの長さ
という方程式を解く必要があるわけですが、
sqrt ( x*x + sinx*sinx ) = リンク長さ
うんむずかしい
。。。
プログラムを書く感じです。
・sin関数1周期を移動量、振幅を移動量にして、m単位でロボットの実現できるサイズで用意します。それを軌道関数(x)にします。
・xを入れます。→軌道関数(x)がもとまります。
・始点を決めます。
・始点からxを少し増やして、軌道関数を求めます。で距離を求めます。
・・・上を距離がいい具合になるまでやります。そのときのxをx1として覚えます。
・x1からすこしずつxを増やし、またちょうどいい距離までやってそれをx2とします。
・同様の方法でx3を決定します。
・・・これで、一番最初のヘビの形が決まりました。
・これを軌道関数1周期分計算します。
・データテーブルとして保存します。
・mbedに入れます。
これで動くんじゃね。
4自由度構成のヘビの移動
ヘビを実際に移動させるには、
ヘビのくねくね、尺取り虫、横転がりが考えられます。
前の記事の通り、yz平面における座標からサーボモータの角度を決定します。

このように、yz座標を取ります。
また、青いベクトルの長さとz軸からの角度の座標ともいえます。
上に書いた3つの移動方法は、青いベクトルを・・・
①水平方向に向け、長さを周期的に変える
②鉛直方向に向け、長さを周期的に変える
③長さを変えずに、ぐるぐる回す
ぐるぐる回すのは胴体中心に対してのものですが、
床から見てみれば、ロボット全体はタイヤの様に転がります。
の3パターンで行えます。
4軸あるので、青いベクトルはロボットに2本あります。タイミングは上手く調整します。
いろいろやってみるしかありません。
実際の動きはコチラ、完成?
とりあえず、動いたんですけど・・・
景気良く動かすのは難しいです。
たぶん景気良く動かす周期関数が存在すると思いますが・・・
そこまでやる気には、ならないのが・・・人の心っていうもの・・・。
うごいたし、へびはひと段落じゃね
ヘビのくねくね、尺取り虫、横転がりが考えられます。
前の記事の通り、yz平面における座標からサーボモータの角度を決定します。
このように、yz座標を取ります。
また、青いベクトルの長さとz軸からの角度の座標ともいえます。
上に書いた3つの移動方法は、青いベクトルを・・・
①水平方向に向け、長さを周期的に変える
②鉛直方向に向け、長さを周期的に変える
③長さを変えずに、ぐるぐる回す
ぐるぐる回すのは胴体中心に対してのものですが、
床から見てみれば、ロボット全体はタイヤの様に転がります。
の3パターンで行えます。
4軸あるので、青いベクトルはロボットに2本あります。タイミングは上手く調整します。
いろいろやってみるしかありません。
実際の動きはコチラ、完成?
とりあえず、動いたんですけど・・・
景気良く動かすのは難しいです。
たぶん景気良く動かす周期関数が存在すると思いますが・・・
そこまでやる気には、ならないのが・・・人の心っていうもの・・・。
うごいたし、へびはひと段落じゃね
4自由度へビのくねくね軌道
ヘビはくねくね動くということで前に進むらしいのです。
なので、くねくね動かす方法を考えます。
くね、と言って右に振り
くね、と言って左に振ればいいのではないでしょうか?
というと、周期的な運動だと考えられるのでsin関数をそのまま入力すればいいのではないか
と考えます。
4自由度2関節のヘビなので、まず片方の関節の1自由度だけを検討します。
例えば、先ほどtheta4の逆関数として
y=f(theta4)を求めたので、
f(theta4) = sin(t)という角度を与えたとします。
ですが、この逆関数はasinなのでsinでは無くなってしまいます。
なので、切り返しが滑らかでは無くなります。
なので
=sin(sin(t))
とかにしてみます。

思惑どおりです。(グラフ上はsinになってしまっていますが)
しかし、このままではだめです。
切り返しが90度であればこのままでもいいのですが、
切り返しが90°出ないとき、もちろんヘビは90度まで曲がっていないようですから、
なので、この結果をそのまま使いません。
このグラフの単位はradですが、
degだと思いなおしたり、クネクネの振幅を命令したいと思ったり、速度0から始めたいと思えば

(この時点で2関節にした時に面倒だなと思い始めるわけですが)
1関節分のくねくねはこれでとりあえず完成です。
2関節目も同様に考えますが、
なにやら、ヘビを見ていると隣り合った関節が、
同時に同じ、あるいは同時に逆ということは無いように思われます。
なので、くねくねには位相のずれを与えるべきです。
例えば、

という感じで、ずらしておきます。
実際は、2本のグラフを書いておいて、縦線を時間軸にそって動かす。
その交点を、その時間の角度として与えます。

これで、くねくね軌道は完成です。
このくねくね軌道は、周期A1、振幅A2、位相のずれA3の3つの変数を持ちます。
実際のところ、yはmaxでd3までしかとれませんので、比として与えられます。
theta3 = arcsin(y/d3)
というところで
Y=y/d3
とします。
Y_1 = sin(%pi*sin([A1]*t)/2 * [A2]/d3)
Y_2 = sin(%pi*sin([A1]*t-[A3])/2 * [A2]/d3)
と与えることにします。
なので、くねくね動かす方法を考えます。
くね、と言って右に振り
くね、と言って左に振ればいいのではないでしょうか?
というと、周期的な運動だと考えられるのでsin関数をそのまま入力すればいいのではないか
と考えます。
4自由度2関節のヘビなので、まず片方の関節の1自由度だけを検討します。
例えば、先ほどtheta4の逆関数として
y=f(theta4)を求めたので、
f(theta4) = sin(t)という角度を与えたとします。
ですが、この逆関数はasinなのでsinでは無くなってしまいます。
なので、切り返しが滑らかでは無くなります。
なので
=sin(sin(t))
とかにしてみます。
思惑どおりです。(グラフ上はsinになってしまっていますが)
しかし、このままではだめです。
切り返しが90度であればこのままでもいいのですが、
切り返しが90°出ないとき、もちろんヘビは90度まで曲がっていないようですから、
なので、この結果をそのまま使いません。
このグラフの単位はradですが、
degだと思いなおしたり、クネクネの振幅を命令したいと思ったり、速度0から始めたいと思えば
(この時点で2関節にした時に面倒だなと思い始めるわけですが)
1関節分のくねくねはこれでとりあえず完成です。
2関節目も同様に考えますが、
なにやら、ヘビを見ていると隣り合った関節が、
同時に同じ、あるいは同時に逆ということは無いように思われます。
なので、くねくねには位相のずれを与えるべきです。
例えば、
という感じで、ずらしておきます。
実際は、2本のグラフを書いておいて、縦線を時間軸にそって動かす。
その交点を、その時間の角度として与えます。
これで、くねくね軌道は完成です。
このくねくね軌道は、周期A1、振幅A2、位相のずれA3の3つの変数を持ちます。
実際のところ、yはmaxでd3までしかとれませんので、比として与えられます。
theta3 = arcsin(y/d3)
というところで
Y=y/d3
とします。
Y_1 = sin(%pi*sin([A1]*t)/2 * [A2]/d3)
Y_2 = sin(%pi*sin([A1]*t-[A3])/2 * [A2]/d3)
と与えることにします。
4自由度ヘビの逆運動学
ひとつ前の記事から続いています。
逆運動学は、
どんな命令でうごかしたいのかで臨機応変にいろんなことを考えればいいものですが、
今回は

中央の車輪あたりにあるy-z平面を使い、3ブロックあるものを真ん中で2つに分けていこうと思います。
クネクネする動作:
前の奴を右に
後ろの奴を左に
みたいな指示を出したいと思えば、中央のブロックからそれぞれの位置姿勢を命令したいということになります。
なので、

端の車輪の中心を、y-z平面に射影したものを見ていきます。
右に振りたければzを増やす、
上にあげたければyを増やすという命令をすればいいことになります。
もちろん「上」とか「右」とかっていう変数を置いたプログラムを作る方が便利かもしれません。
さて、順運動学をもう一回やります。
まんなかから考えるので、
同次変換行列は

この3つです。
先端までまとめると

私が命令したいのはy座標とz座標です。
最右列の上から2番目と3番目以外に興味はありません。
sin(theta4)*d3=y
と
-sin(theta3)*cos(theta4)*d3=z
という式です。
変数は、zとyとtheta3とtheta4です。
zとyには、どのくらい上にあげたいのか、右に曲げたいのか
ということに合わせて好きな数字を入れればいいと思います。
それでtheta3とtheta4はどうなるのかっていうところが気になります。
で、どうするのかっていうのは人の好きなのですが
theta4に関しては、変数1つの非線形方程式なのでいろんな方法が簡単に出来ます。
①arcsinをつかう
②数値計算で収束をまつ
③サインと角度のデータテーブルからそれっぽいのを選ぶ
ま、あ、すきな方法でやります。
①でやります。
何にも考えずに①でやります。
theta4 = arcsin(y/d3) です。
なぜなら、theta4の可動範囲は±90°だからです。
arcsinも同じ範囲をサポートしています。
ではtheta3をやります。
theta4が計算してからtheta3を計算すれば
cos(theta4)は定数です。
で、再びarcsinをやります。
theta3 = -arcsin(z/d3cos(theta4)) です。
theta3とtheta4が決まりました。
●theta3 = -arcsin(z/d3cos(theta4))
●theta4 = arcsin(y/d3)
この角度をサーボモータに指示すればいいわけですね。
逆運動学は、
どんな命令でうごかしたいのかで臨機応変にいろんなことを考えればいいものですが、
今回は
中央の車輪あたりにあるy-z平面を使い、3ブロックあるものを真ん中で2つに分けていこうと思います。
クネクネする動作:
前の奴を右に
後ろの奴を左に
みたいな指示を出したいと思えば、中央のブロックからそれぞれの位置姿勢を命令したいということになります。
なので、
端の車輪の中心を、y-z平面に射影したものを見ていきます。
右に振りたければzを増やす、
上にあげたければyを増やすという命令をすればいいことになります。
もちろん「上」とか「右」とかっていう変数を置いたプログラムを作る方が便利かもしれません。
さて、順運動学をもう一回やります。
まんなかから考えるので、
同次変換行列は
この3つです。
先端までまとめると
私が命令したいのはy座標とz座標です。
最右列の上から2番目と3番目以外に興味はありません。
sin(theta4)*d3=y
と
-sin(theta3)*cos(theta4)*d3=z
という式です。
変数は、zとyとtheta3とtheta4です。
zとyには、どのくらい上にあげたいのか、右に曲げたいのか
ということに合わせて好きな数字を入れればいいと思います。
それでtheta3とtheta4はどうなるのかっていうところが気になります。
で、どうするのかっていうのは人の好きなのですが
theta4に関しては、変数1つの非線形方程式なのでいろんな方法が簡単に出来ます。
①arcsinをつかう
②数値計算で収束をまつ
③サインと角度のデータテーブルからそれっぽいのを選ぶ
ま、あ、すきな方法でやります。
①でやります。
何にも考えずに①でやります。
theta4 = arcsin(y/d3) です。
なぜなら、theta4の可動範囲は±90°だからです。
arcsinも同じ範囲をサポートしています。
ではtheta3をやります。
theta4が計算してからtheta3を計算すれば
cos(theta4)は定数です。
で、再びarcsinをやります。
theta3 = -arcsin(z/d3cos(theta4)) です。
theta3とtheta4が決まりました。
●theta3 = -arcsin(z/d3cos(theta4))
●theta4 = arcsin(y/d3)
この角度をサーボモータに指示すればいいわけですね。
4自由度ヘビの順運動学
割と一般的な方法で運動学をすすめるにあたり、簡単な自由度でまとめておく記事です。

題材は4自由度のヘビ
2軸ごとに直交
左から始まるとして
d1-θ1θ2-d2-θ3θ4-d3
という様に、リンク長さと、回転軸があります。
さて、座標系は写真の姿勢で→向きをx軸、鉛直↑向きをy軸、手前に伸びる奴をz軸として、
θ1-y軸
θ2-z軸
θ3-y軸
θ4-z軸
という回転軸を持ちます。
左側のリンク端をロボットの基準座標系
5つの同次変換行列をつかって位置姿勢を表現します。

maximaを使います。
同次変換行列は回転行列の右に位置ベクトルをかくという方法です。
なので、下の行は便宜上存在しているだけなので0,0,0,1です。
どんな時の0,0,0,1です。
d1は左端からθ1θ2までの距離、d2はそこからθ3θ4までの距離、d3はそこから右端までです。
同次変換行列は、進んでから姿勢を変換させていると捉えていいので、T12はd1とθ1を表現します。
T23はθ1からθ2までの距離を持つことができますが、直交軸なので最右列は0,0,0,1となってます。
単純なマニピュレータとして
基準座標系から右端の、位置姿勢は

という同次変換行列にまとめられます。
4つだけのモータにこれだけ紙面を必要とするというのは、
やる気が無くなります。
手で書いていたら人生というのは短すぎるでしょう。
この式の表し方にはまだまだ改善の余地があると将来をきたいします。
これが、教科書に書いてある順運動学ですね。
題材は4自由度のヘビ
2軸ごとに直交
左から始まるとして
d1-θ1θ2-d2-θ3θ4-d3
という様に、リンク長さと、回転軸があります。
さて、座標系は写真の姿勢で→向きをx軸、鉛直↑向きをy軸、手前に伸びる奴をz軸として、
θ1-y軸
θ2-z軸
θ3-y軸
θ4-z軸
という回転軸を持ちます。
左側のリンク端をロボットの基準座標系
5つの同次変換行列をつかって位置姿勢を表現します。
maximaを使います。
同次変換行列は回転行列の右に位置ベクトルをかくという方法です。
なので、下の行は便宜上存在しているだけなので0,0,0,1です。
どんな時の0,0,0,1です。
d1は左端からθ1θ2までの距離、d2はそこからθ3θ4までの距離、d3はそこから右端までです。
同次変換行列は、進んでから姿勢を変換させていると捉えていいので、T12はd1とθ1を表現します。
T23はθ1からθ2までの距離を持つことができますが、直交軸なので最右列は0,0,0,1となってます。
単純なマニピュレータとして
基準座標系から右端の、位置姿勢は
という同次変換行列にまとめられます。
4つだけのモータにこれだけ紙面を必要とするというのは、
やる気が無くなります。
手で書いていたら人生というのは短すぎるでしょう。
この式の表し方にはまだまだ改善の余地があると将来をきたいします。
これが、教科書に書いてある順運動学ですね。
プロフィール
HN:
Adel
年齢:
36
性別:
男性
誕生日:
1989/09/17
職業:
会社員
趣味:
モチベーション探し
自己紹介:
ロボットつくるのが夢
最新記事
(07/15)
(02/17)
(05/28)
(04/25)
(02/19)
カテゴリー
ブログ内検索
アクセス解析

