くねくね移動がうまくいかないので、
上手くいくくねくね軌道を幾何学的に決定します。
偉い人から
「蛇行軌道にすべての車輪がのっかっていて、接線の方向を向いているべき」
とのお話を頂きましたので、それを検討します。
①sin関数にのっかる
②車輪が軌道にのるように角度を決定する
③もうひとつの車輪も同様に角度を決定する
だと思いましたが！
良く考えると・・・
平面的には2自由度、3節あります。
1個目の車輪は、のせられます。
2個目は？
1個目の車輪の位置と姿勢、例えば、
x=0,y=0,θ=45°
とかだとします。
すると、1個目の関節の位置は
x=cos45,y=sin45
です。
そこから1つめのモータの角度を変えて、
2個目の車輪を軌道に乗るように決めます。
すると、角度は接線方向になりません？！
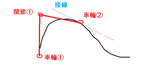
困りました。
モータ1個では、位置&角度を決めるのは無理で、どちらか一方しか決められません。
困りました。
でもまあ、仕方ないので、接線は諦めることにしまして
各関節が、軌道に乗るような角度を決めていこうと思います。
と思いましたが、これも意外と大変。
3節あるヘビロボットの1節目のリンクだけを考えます。
このリンクの両端点がsin関数上に乗ってくれればいいのですが・・・
どうやって載せるんでしょう？
リンクを直線だと思って、x軸からの傾きを決める他ありません。
これはつまり、中心がsin関数上の円とsin関数の交点を求める問題です。
が、そのとき方については僕は収束計算以外の方法を知りません。
例えば
y=0,x=0からx=x,y=sinx
までの距離は、平方根の中に三角関数の2乗があるというこれまた難しい。
で、
その距離＝リンクの長さ
という方程式を解く必要があるわけですが、
sqrt ( x*x + sinx*sinx ) = リンク長さ
うんむずかしい
。。。
プログラムを書く感じです。
・sin関数１周期を移動量、振幅を移動量にして、ｍ単位でロボットの実現できるサイズで用意します。それを軌道関数(x)にします。
・xを入れます。→軌道関数(x)がもとまります。
・始点を決めます。
・始点からｘを少し増やして、軌道関数を求めます。で距離を求めます。
・・・上を距離がいい具合になるまでやります。そのときのxをx1として覚えます。
・x1からすこしずつxを増やし、またちょうどいい距離までやってそれをx2とします。
・同様の方法でx3を決定します。
・・・これで、一番最初のヘビの形が決まりました。
・これを軌道関数１周期分計算します。
・データテーブルとして保存します。
・mbedに入れます。
これで動くんじゃね。
[0回]
PR
