創生×⇒創成○
だそうです。
大きな問題ですね。
シミュレーションに迫られておりまして、非線形微分方程式を積分したくなっております。
解析解は出ませんどころか、点群データなわけで。
シミュレーションに迫られて います。
5年前にこのブログでもルンゲクッタ法にふれていましたが。
すっかり忘れたのでもう一度記事にします。
参考サイト様簡単なシミュならオイラー法を使います。
dx/dt=Ax
であれば,刻みのステップをhとして
x1=x0+A*x0*h
という漸化式なので次々と計算すればいいです。
ただ、1次の傾きを積分していくので誤差が積もります。
そこで誤差の少ない方法が世間には広まっているのです。
その例としてルンゲクッタを選びました。
↑の式で進めると
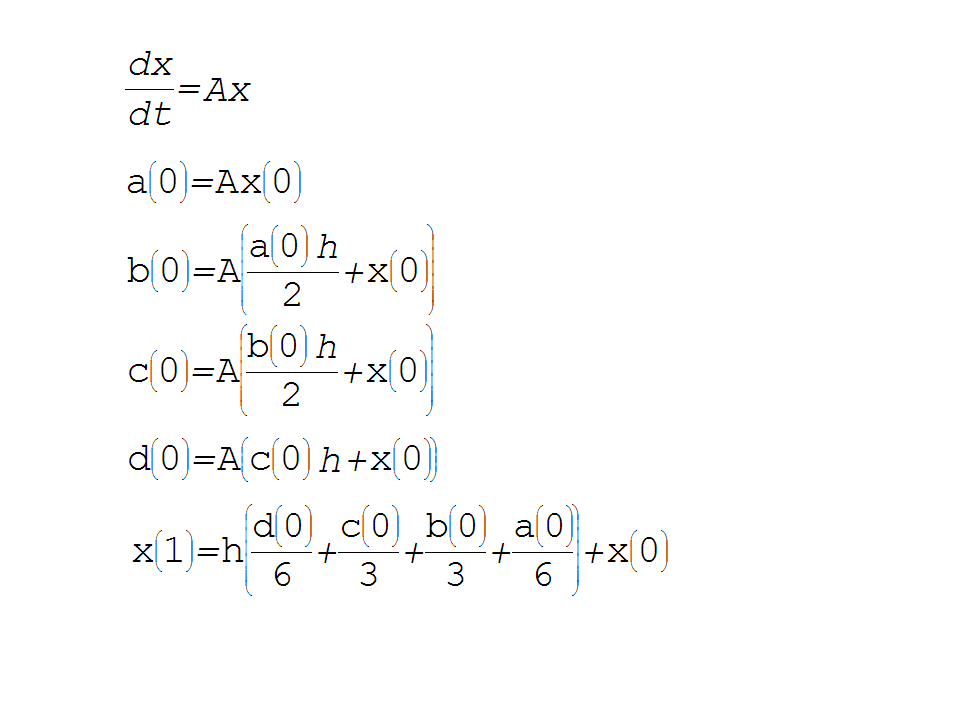a b c dという4つの係数から、理想的な傾きを求めるようです。
数値計算の教科書とかだと、一般的な常微分方程式を念頭に置いているので、単純な式だと返って分かりづらいものでした。
引数？がだいぶ減るので簡単です。
例えば、
dx/dt=A*t*x
みたいな場合であれば、もう少し教科書寄りの式に成ります。
で、どのくらい精度がいいかということですが
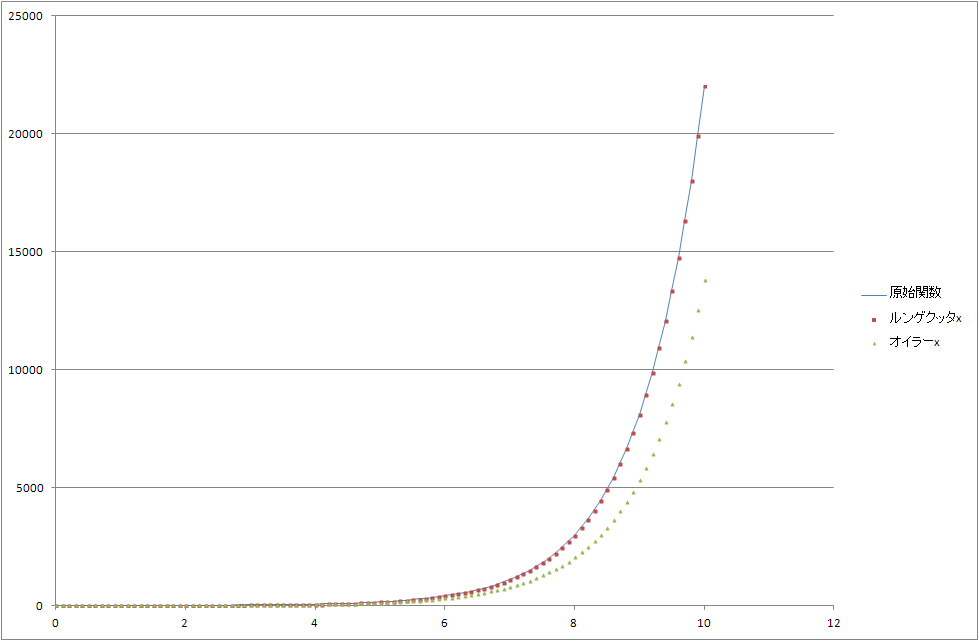
ただのexpカーブが解析解となりますが、このようにオイラーだと離れていくところが付いていくわけです。
でもって、簡単なところはこの辺で。
もう少し応用の利く例を置いておきます。
運動方程式であれば、2階の微分方程式だと思います。
d^2x/dt^2=Bx
みたいな。
Bが負であれば単振動です。
計算は、状態方程式のように2つに分けて、y1,y2の連立の１階微分方程式にします。
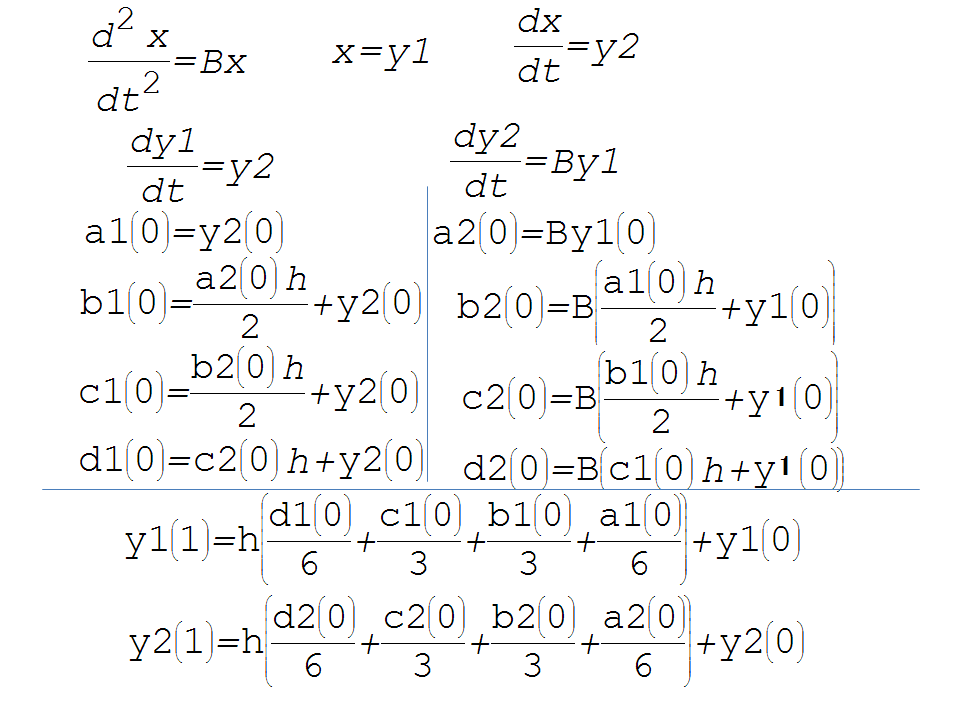
さっきと同様にa b c d を計算しますが、
y1とy2の流れを交互にやることに注意します。
y2のb、つまりb2はa1を使って計算する必要があります。
少し複雑です。
計算結果です。
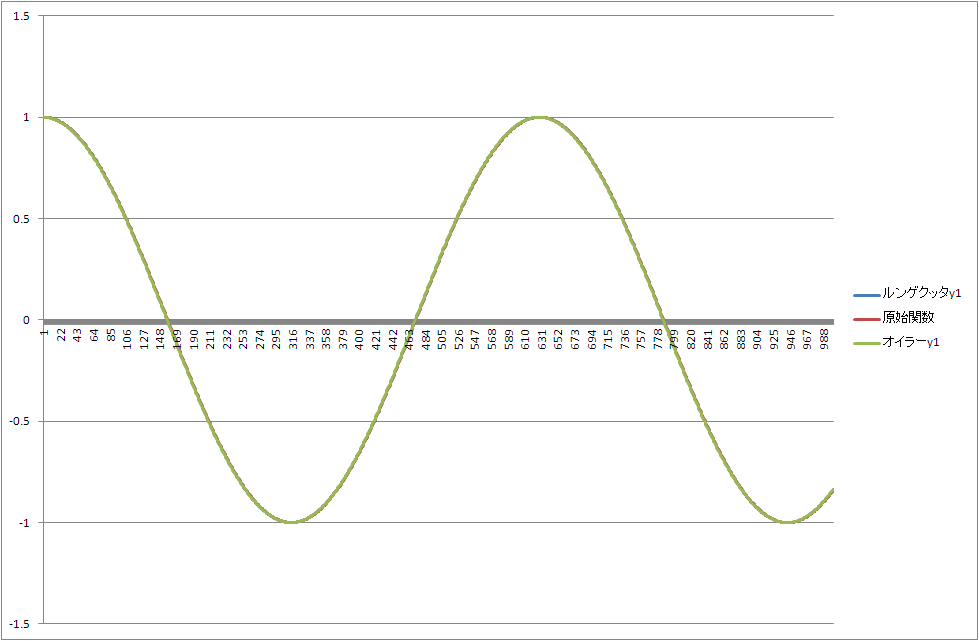B=-1だと思いますが。
ざっくりこんな状態です。
オイラーでもほとんど一緒です。
ですが、解析解との差分をみると
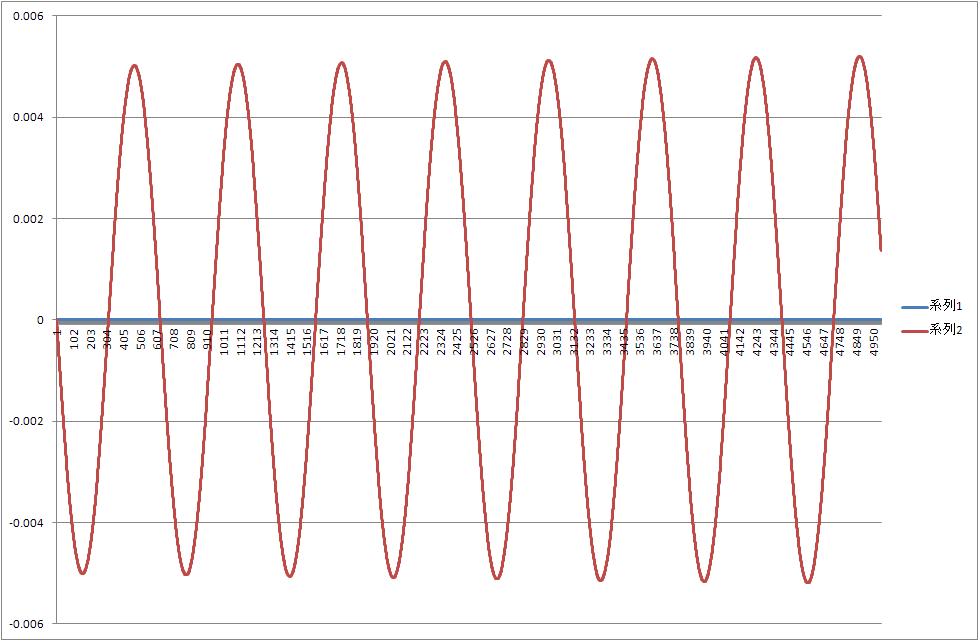このようになっているので、ルンゲクッタの頑張りようがわかるのではないでしょうか。
ダウンロード元エクセルを置いておきます。内容は整理していませんのですいません。
さて、２階だろうが、連立だろうができるようになりましたので、
多質点の運動方程式に手が届きます。
それはまた今度。
[0回]
PR
