歯車どうやって作るシリーズ再開です。
ぜんかい、図形を少しずつずらしていくと曲線が見えてくる⇒これが歯だ
という展開でしたが、ではその曲線そのものはどんな関数としてあらわされるのか？
で、ネットサーフィンの果てに"包絡線"というものを見つけました。
参考サイト様
http://hooktail.sub.jp/mathInPhys/envelope/直線をずらしていく
線が一杯引ける
さて、その線群はどんな曲線を描くか？
現在の理解レベル：
①曲線に一つ変数を加えて、ずらすことを表現する ← 歯車は１自由度だから当然か…
②その曲線群関数を加えた変数で偏微分する
③連立させて変数を消す
④勝利
・・・☆
というのは難しいので、既にある曲線から接線の群を取り出し、曲線を見いだすという実験をしてみます。
２次関数は
てなかんじで接線の方程式がもとめられますね！
接線を一杯描いてみる＆２次関数と重ねる
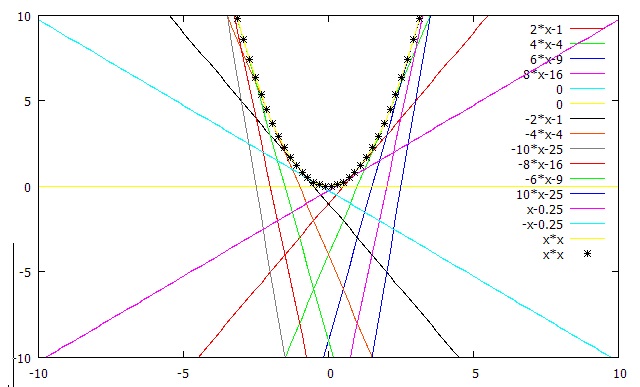
JPEGで張り付けるとカスみたいな画質ですね。
ちなみにθを0.5:5まで正負いれてみた接線と、
２次関数は分かりづらかったのでアスタリスクで出しました。
間違えた線も入ってますけど、
まーこんなかんじっていうイメージを掴むには充分と思います。
では、やってみますか
①曲線に一つ変数を加えて、ずらすことを表現する ← 歯車は１自由度だから当然か…
②その曲線群関数を加えた変数で偏微分する
③連立させて変数を消す
④勝利
勝利しましたね。
世の中大したことありません。
はて、接線群の関数の偏微分とはどういう意味でしょうか？
偏導関数なので、接した時の向きを言っています。
で、それは(x,y,θ)を通ると言っているのです。
・・・よくわかりません。偏微分を勉強しましょう。
[0回]
PR
