明日の設計図
たまにロボットを考えるブログ・・・。
[PR]
×
[PR]上記の広告は3ヶ月以上新規記事投稿のないブログに表示されています。新しい記事を書く事で広告が消えます。
bluetooth ドライバを入れて イヤホンを使う
ソニーのSBH82Dという、オープンイヤーワイヤレスヘッドステレオヘッドセットを使うために苦労したのでブログにします。
PCはbluetooth内臓のthinkpadです。win7 SP1です。
○できない様子
・イヤホンをペアリングモードにする
・bluetoothデバイスの追加からSBH82Dを探して接続する
・ドライバのインストールが始まる
・ドライバが見つからない
使えない・・・
○できる様子
・BluetoothAudio ドライバなどとググる
・インテル@・・・・
・インストール用のexeをダウンロードする
・管理者実行する
・すごい時間がかかる
・サービスが停止できません、権限を確認云々がでる。
・bluetooth media service が停止できないとでる。
・msconfigから見ると停止中になっていて、そこからアクセスは何もできない
・インストールをキャンセルする
・PCを再起動する
・タスクマネージャのサービスから即刻、bluetooth media serviceを停止する
・インストーラを管理者実行する
・すごい時間がかかる→インストールできる
・イヤホンをペアリングモードにする
・デバイスの追加からSBH82Dを追加する
・ドライバのインストールが成功する
・デバイスサービスから接続する
・サウンドからBluetoothheadphonesが選べるようになる
・えらぶ
・適当に音を出す
PCはbluetooth内臓のthinkpadです。win7 SP1です。
○できない様子
・イヤホンをペアリングモードにする
・bluetoothデバイスの追加からSBH82Dを探して接続する
・ドライバのインストールが始まる
・ドライバが見つからない
使えない・・・
○できる様子
・BluetoothAudio ドライバなどとググる
・インテル@・・・・
・インストール用のexeをダウンロードする
・管理者実行する
・すごい時間がかかる
・サービスが停止できません、権限を確認云々がでる。
・bluetooth media service が停止できないとでる。
・msconfigから見ると停止中になっていて、そこからアクセスは何もできない
・インストールをキャンセルする
・PCを再起動する
・タスクマネージャのサービスから即刻、bluetooth media serviceを停止する
・インストーラを管理者実行する
・すごい時間がかかる→インストールできる
・イヤホンをペアリングモードにする
・デバイスの追加からSBH82Dを追加する
・ドライバのインストールが成功する
・デバイスサービスから接続する
・サウンドからBluetoothheadphonesが選べるようになる
・えらぶ
・適当に音を出す
PR
有限角度のノンバックラッシプーリ伝達
簡単な部品でノンバックラッシ伝達ができないかと思ってチャレンジしました。
2本のテグス間にテンションをかけます。
小プーリで270deg動きます。

忘備録
回転の伝達なので、歯車かプーリかの2択です。
バックラッシのない歯車は超激レアなので重課金です。
タイミングベルトでプーリも面倒です。
ノンバックラッシにしようと思うと、いずれの場合も専門の加工が必要なので面倒です。
状況を有限角度に絞って簡単にすれば
・リンク
という選択肢があります。
が、リンクはノンバックラッシではありません。
重い部品が増えます。
構造物が増えることは作るのがめんどくさくなります。
結果として、リンクとプーリを組み合わせた感じにしました。
以下、こんな感じに作る。
2本のナイロンテグスをそこそこ同じ長さでつけて、
プーリを動かしてテンション調整して完成。
材料
3Dプリント部品4点
M3のねじが2本
6900ZZが4個
M2のねじが4本
ナイロンテグス適当




2本のテグス間にテンションをかけます。
小プーリで270deg動きます。
忘備録
回転の伝達なので、歯車かプーリかの2択です。
バックラッシのない歯車は超激レアなので重課金です。
タイミングベルトでプーリも面倒です。
ノンバックラッシにしようと思うと、いずれの場合も専門の加工が必要なので面倒です。
状況を有限角度に絞って簡単にすれば
・リンク
という選択肢があります。
が、リンクはノンバックラッシではありません。
重い部品が増えます。
構造物が増えることは作るのがめんどくさくなります。
結果として、リンクとプーリを組み合わせた感じにしました。
以下、こんな感じに作る。
2本のナイロンテグスをそこそこ同じ長さでつけて、
プーリを動かしてテンション調整して完成。
材料
3Dプリント部品4点
M3のねじが2本
6900ZZが4個
M2のねじが4本
ナイロンテグス適当
実行ファイルにドラッグアンドドロップする。
忘備録
Cでテキストファイルを処理したいとき、アドレスのパスをどうやって渡すかいつも面倒だと思っていました。
で、よく考えると実行形式のファイルに乗っけて起動するタイプのソフトってありますよね。
だからそういうのできるんだと思ってググりました。
http://achapi2718.blogspot.jp/2012/06/c_1002.html
簡潔にまとめていただいているサイト様がありましたので記録しておきます。
後日、トライします。
Cでテキストファイルを処理したいとき、アドレスのパスをどうやって渡すかいつも面倒だと思っていました。
で、よく考えると実行形式のファイルに乗っけて起動するタイプのソフトってありますよね。
だからそういうのできるんだと思ってググりました。
http://achapi2718.blogspot.jp/2012/06/c_1002.html
簡潔にまとめていただいているサイト様がありましたので記録しておきます。
後日、トライします。
pythonはじめました
超素人が、pythonでGUI開発を軌道に乗せるまで備忘録
①いろいろググるとanacondaをインストールすることになります。
https://www.continuum.io/downloads
windows版の32bitを10分ぐらいでダウンロードして、
実行して
30分弱ぐらいのインストールをします。
この時点で時間がかかりすぎです。10人以上のウルトラマンが帰ってしまうでしょう。
もうそれだけで環境の準備は終わります。
②いろいろインストールされて、何をやればいいのか分からなくなります。
で何をすればいいかというと
スタートメニュー→あなこんだ→jupyter notebook
を開きます。
そうすると、ブラウザの新しいたぶとして開かれます。
マイドキュメントとかが見えると思うので、
エクスプローラとかでpython用のフォルダを作っておく。
こちらが参考になります。
http://pythondatascience.plavox.info/python%E3%81%AE%E9%96%8B%E7%99%BA%E7%92%B0%E5%A2%83/jupyter-notebook%E3%82%92%E4%BD%BF%E3%81%A3%E3%81%A6%E3%81%BF%E3%82%88%E3%81%86/
と思いきや、ブラウザは立ち上がらないです。
なんでか分かりません。
で、アナコンダナビゲーターというのを開きます。
そこから、jupyternotebookをローンチュします。
あとは大丈夫です。
③pythonのコードを書いて、shift enterします。
でき上がりです。
④GUIをします。
guiする方法は数多ある様ですが、アナコンダにはPyQt5が盛り込まれていました。
で、
http://d.hatena.ne.jp/mFumi/20141112/1415806010
こちらのサイトのコピペを実行してみます。
普通にできます。
⑤エクストラステージ
新しい環境を入れる時は順風満帆ではないのが常です。
実行できるんですけども、
The kernel appears to have died. It will restart automatically.
とjupyterさんに言われます。
で、
http://stackoverflow.com/questions/40094086/python-kernel-dies-for-second-run-of-pyqt5-gui
こちらを参考に
app = QApplication(sys.argv)
がいけないらしいので
app = QApplication.instance()
if app is None:
app = QApplication(sys.argv)
とします。
終わり。
①いろいろググるとanacondaをインストールすることになります。
https://www.continuum.io/downloads
windows版の32bitを10分ぐらいでダウンロードして、
実行して
30分弱ぐらいのインストールをします。
この時点で時間がかかりすぎです。10人以上のウルトラマンが帰ってしまうでしょう。
もうそれだけで環境の準備は終わります。
②いろいろインストールされて、何をやればいいのか分からなくなります。
で何をすればいいかというと
スタートメニュー→あなこんだ→jupyter notebook
を開きます。
そうすると、ブラウザの新しいたぶとして開かれます。
マイドキュメントとかが見えると思うので、
エクスプローラとかでpython用のフォルダを作っておく。
こちらが参考になります。
http://pythondatascience.plavox.info/python%E3%81%AE%E9%96%8B%E7%99%BA%E7%92%B0%E5%A2%83/jupyter-notebook%E3%82%92%E4%BD%BF%E3%81%A3%E3%81%A6%E3%81%BF%E3%82%88%E3%81%86/
と思いきや、ブラウザは立ち上がらないです。
なんでか分かりません。
で、アナコンダナビゲーターというのを開きます。
そこから、jupyternotebookをローンチュします。
あとは大丈夫です。
③pythonのコードを書いて、shift enterします。
でき上がりです。
④GUIをします。
guiする方法は数多ある様ですが、アナコンダにはPyQt5が盛り込まれていました。
で、
http://d.hatena.ne.jp/mFumi/20141112/1415806010
こちらのサイトのコピペを実行してみます。
普通にできます。
⑤エクストラステージ
新しい環境を入れる時は順風満帆ではないのが常です。
実行できるんですけども、
The kernel appears to have died. It will restart automatically.
とjupyterさんに言われます。
で、
http://stackoverflow.com/questions/40094086/python-kernel-dies-for-second-run-of-pyqt5-gui
こちらを参考に
app = QApplication(sys.argv)
がいけないらしいので
app = QApplication.instance()
if app is None:
app = QApplication(sys.argv)
とします。
終わり。
ルンゲクッタ法で微分方程式(単振動)を積分
創生×⇒創成○
だそうです。
大きな問題ですね。
シミュレーションに迫られておりまして、非線形微分方程式を積分したくなっております。
解析解は出ませんどころか、点群データなわけで。
シミュレーションに迫られて います。
5年前にこのブログでもルンゲクッタ法にふれていましたが。
すっかり忘れたのでもう一度記事にします。
参考サイト様
簡単なシミュならオイラー法を使います。
dx/dt=Ax
であれば,刻みのステップをhとして
x1=x0+A*x0*h
という漸化式なので次々と計算すればいいです。
ただ、1次の傾きを積分していくので誤差が積もります。
そこで誤差の少ない方法が世間には広まっているのです。
その例としてルンゲクッタを選びました。
↑の式で進めると
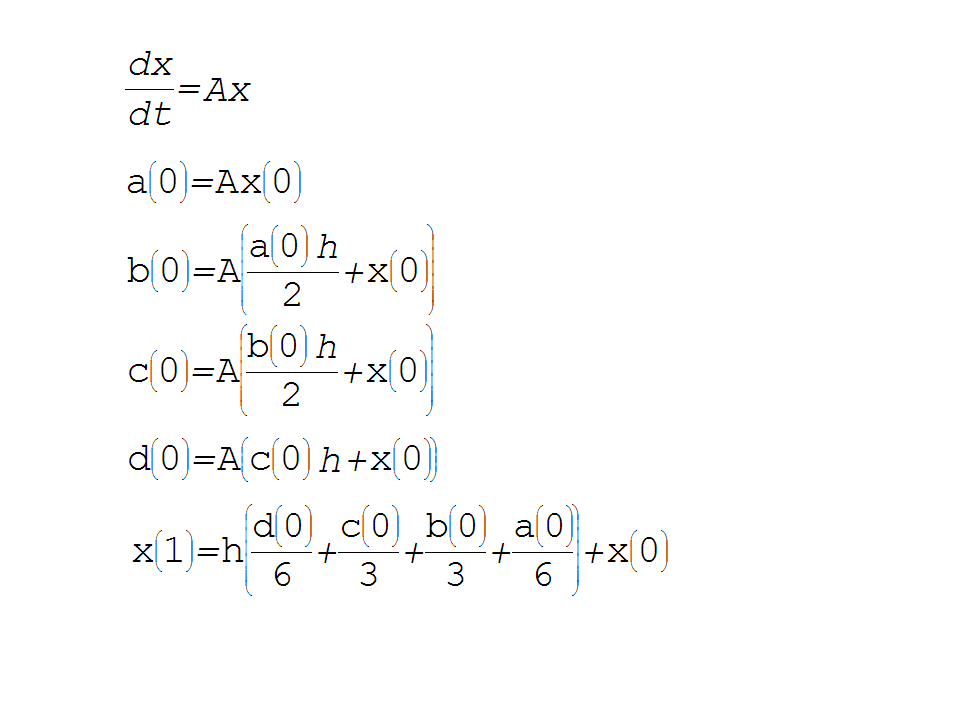 a b c dという4つの係数から、理想的な傾きを求めるようです。
a b c dという4つの係数から、理想的な傾きを求めるようです。
数値計算の教科書とかだと、一般的な常微分方程式を念頭に置いているので、単純な式だと返って分かりづらいものでした。
引数?がだいぶ減るので簡単です。
例えば、
dx/dt=A*t*x
みたいな場合であれば、もう少し教科書寄りの式に成ります。
で、どのくらい精度がいいかということですが
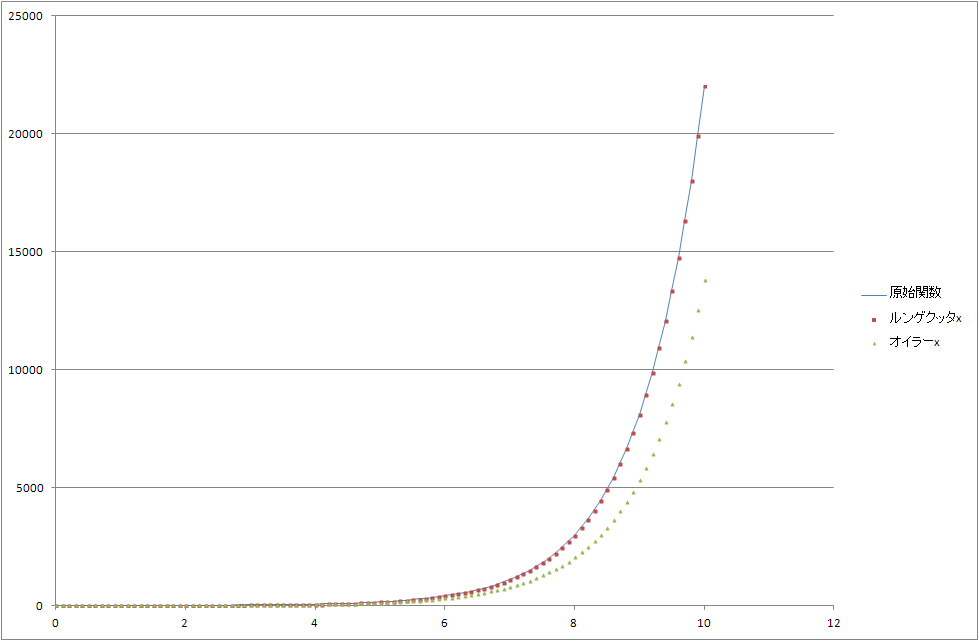
ただのexpカーブが解析解となりますが、このようにオイラーだと離れていくところが付いていくわけです。
でもって、簡単なところはこの辺で。
もう少し応用の利く例を置いておきます。
運動方程式であれば、2階の微分方程式だと思います。
d^2x/dt^2=Bx
みたいな。
Bが負であれば単振動です。
計算は、状態方程式のように2つに分けて、y1,y2の連立の1階微分方程式にします。
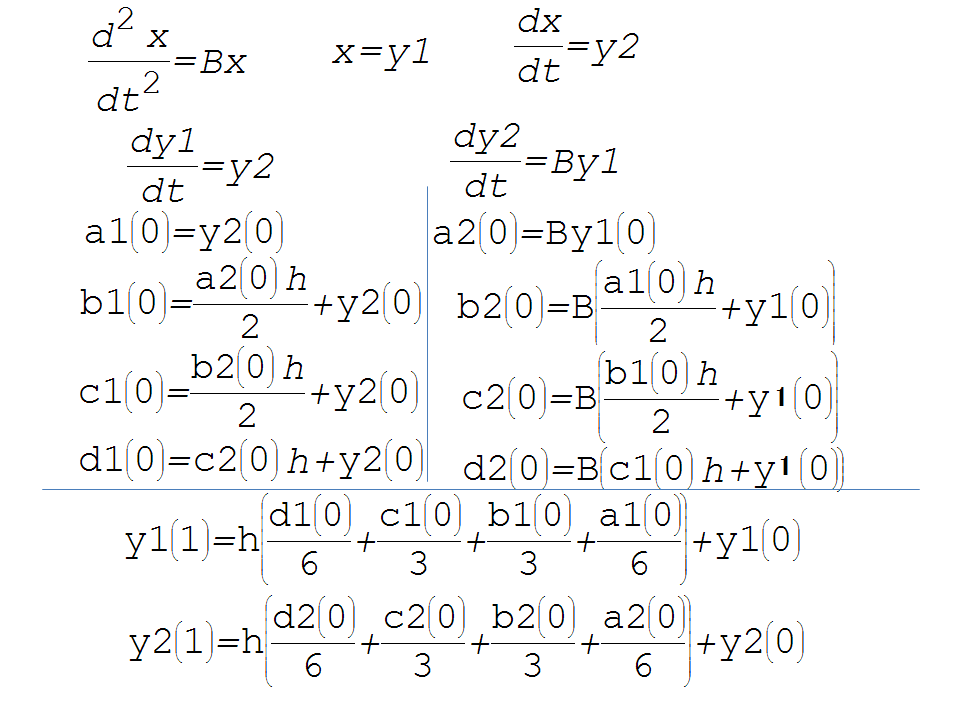
さっきと同様にa b c d を計算しますが、
y1とy2の流れを交互にやることに注意します。
y2のb、つまりb2はa1を使って計算する必要があります。
少し複雑です。
計算結果です。
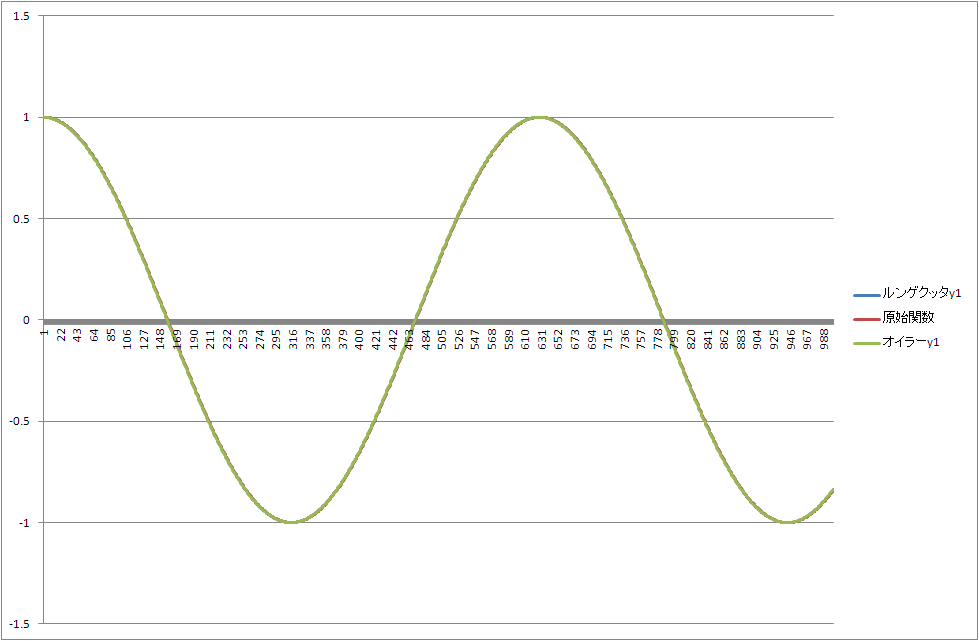 B=-1だと思いますが。
B=-1だと思いますが。
ざっくりこんな状態です。
オイラーでもほとんど一緒です。
ですが、解析解との差分をみると
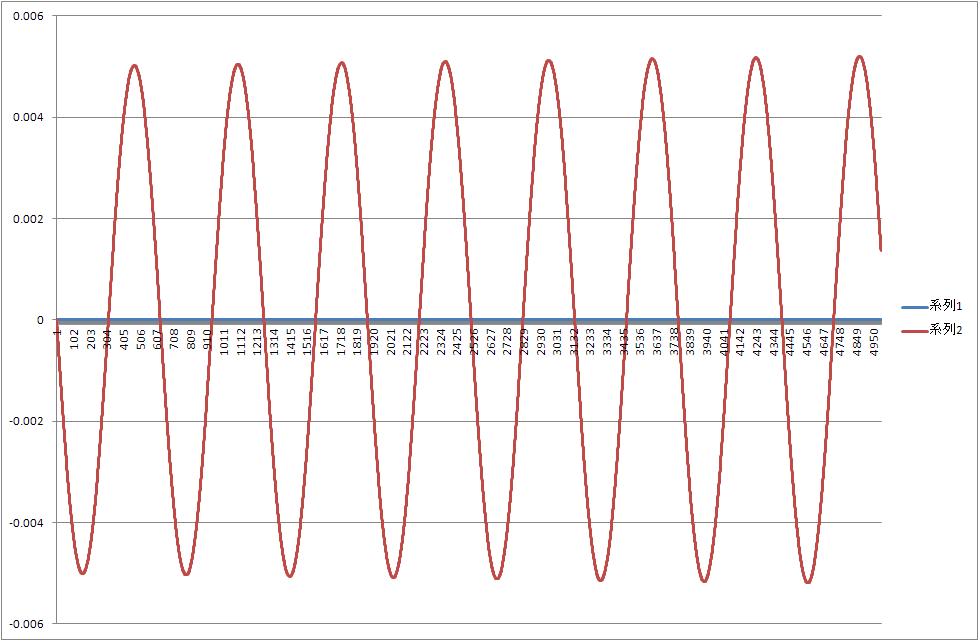 このようになっているので、ルンゲクッタの頑張りようがわかるのではないでしょうか。
このようになっているので、ルンゲクッタの頑張りようがわかるのではないでしょうか。
ダウンロード
元エクセルを置いておきます。内容は整理していませんのですいません。
さて、2階だろうが、連立だろうができるようになりましたので、
多質点の運動方程式に手が届きます。
それはまた今度。
だそうです。
大きな問題ですね。
シミュレーションに迫られておりまして、非線形微分方程式を積分したくなっております。
解析解は出ませんどころか、点群データなわけで。
シミュレーションに迫られて います。
5年前にこのブログでもルンゲクッタ法にふれていましたが。
すっかり忘れたのでもう一度記事にします。
参考サイト様
簡単なシミュならオイラー法を使います。
dx/dt=Ax
であれば,刻みのステップをhとして
x1=x0+A*x0*h
という漸化式なので次々と計算すればいいです。
ただ、1次の傾きを積分していくので誤差が積もります。
そこで誤差の少ない方法が世間には広まっているのです。
その例としてルンゲクッタを選びました。
↑の式で進めると
数値計算の教科書とかだと、一般的な常微分方程式を念頭に置いているので、単純な式だと返って分かりづらいものでした。
引数?がだいぶ減るので簡単です。
例えば、
dx/dt=A*t*x
みたいな場合であれば、もう少し教科書寄りの式に成ります。
で、どのくらい精度がいいかということですが
ただのexpカーブが解析解となりますが、このようにオイラーだと離れていくところが付いていくわけです。
でもって、簡単なところはこの辺で。
もう少し応用の利く例を置いておきます。
運動方程式であれば、2階の微分方程式だと思います。
d^2x/dt^2=Bx
みたいな。
Bが負であれば単振動です。
計算は、状態方程式のように2つに分けて、y1,y2の連立の1階微分方程式にします。
さっきと同様にa b c d を計算しますが、
y1とy2の流れを交互にやることに注意します。
y2のb、つまりb2はa1を使って計算する必要があります。
少し複雑です。
計算結果です。
ざっくりこんな状態です。
オイラーでもほとんど一緒です。
ですが、解析解との差分をみると
ダウンロード
元エクセルを置いておきます。内容は整理していませんのですいません。
さて、2階だろうが、連立だろうができるようになりましたので、
多質点の運動方程式に手が届きます。
それはまた今度。
歯車創生2
歯車どうやって作るシリーズ再開です。
ぜんかい、図形を少しずつずらしていくと曲線が見えてくる⇒これが歯だ
という展開でしたが、ではその曲線そのものはどんな関数としてあらわされるのか?
で、ネットサーフィンの果てに"包絡線"というものを見つけました。
参考サイト様http://hooktail.sub.jp/mathInPhys/envelope/
直線をずらしていく
線が一杯引ける
さて、その線群はどんな曲線を描くか?
現在の理解レベル:
①曲線に一つ変数を加えて、ずらすことを表現する ← 歯車は1自由度だから当然か…
②その曲線群関数を加えた変数で偏微分する
③連立させて変数を消す
④勝利
・・・☆
というのは難しいので、既にある曲線から接線の群を取り出し、曲線を見いだすという実験をしてみます。
2次関数は
 てなかんじで接線の方程式がもとめられますね!
てなかんじで接線の方程式がもとめられますね!
接線を一杯描いてみる&2次関数と重ねる
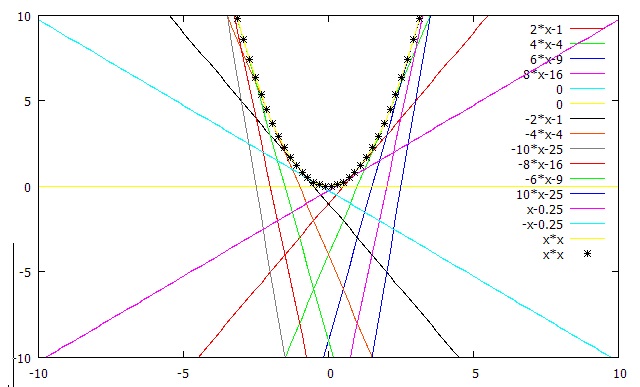
JPEGで張り付けるとカスみたいな画質ですね。
ちなみにθを0.5:5まで正負いれてみた接線と、
2次関数は分かりづらかったのでアスタリスクで出しました。
間違えた線も入ってますけど、
まーこんなかんじっていうイメージを掴むには充分と思います。
では、やってみますか
①曲線に一つ変数を加えて、ずらすことを表現する ← 歯車は1自由度だから当然か…
②その曲線群関数を加えた変数で偏微分する
③連立させて変数を消す
④勝利
 勝利しましたね。
勝利しましたね。
世の中大したことありません。
はて、接線群の関数の偏微分とはどういう意味でしょうか?
偏導関数なので、接した時の向きを言っています。
で、それは(x,y,θ)を通ると言っているのです。
・・・よくわかりません。偏微分を勉強しましょう。
ぜんかい、図形を少しずつずらしていくと曲線が見えてくる⇒これが歯だ
という展開でしたが、ではその曲線そのものはどんな関数としてあらわされるのか?
で、ネットサーフィンの果てに"包絡線"というものを見つけました。
参考サイト様http://hooktail.sub.jp/mathInPhys/envelope/
直線をずらしていく
線が一杯引ける
さて、その線群はどんな曲線を描くか?
現在の理解レベル:
①曲線に一つ変数を加えて、ずらすことを表現する ← 歯車は1自由度だから当然か…
②その曲線群関数を加えた変数で偏微分する
③連立させて変数を消す
④勝利
・・・☆
というのは難しいので、既にある曲線から接線の群を取り出し、曲線を見いだすという実験をしてみます。
2次関数は
接線を一杯描いてみる&2次関数と重ねる
JPEGで張り付けるとカスみたいな画質ですね。
ちなみにθを0.5:5まで正負いれてみた接線と、
2次関数は分かりづらかったのでアスタリスクで出しました。
間違えた線も入ってますけど、
まーこんなかんじっていうイメージを掴むには充分と思います。
では、やってみますか
①曲線に一つ変数を加えて、ずらすことを表現する ← 歯車は1自由度だから当然か…
②その曲線群関数を加えた変数で偏微分する
③連立させて変数を消す
④勝利
世の中大したことありません。
はて、接線群の関数の偏微分とはどういう意味でしょうか?
偏導関数なので、接した時の向きを言っています。
で、それは(x,y,θ)を通ると言っているのです。
・・・よくわかりません。偏微分を勉強しましょう。
歯車創生1
★ロボットを作っていくうえでギアが必要ですが、ギアはどうやって作るんでしょう?
・そもそも歯の形状って何なの。
・インヴォリュートってなんなの。
・なんでうまくかみ合うの。
などなどいろんな不思議と戦う必要があります。
かなり世の中は不思議でいっぱいです。
ググってみると加工法は分かります。
ラックをつかうのとピニオンカッターをつかうのと・・・いろいろです。
というわけで、まずはどうやって歯形を得るかを考えてみます。
歯形が得られれば、NCで作るとか3Dプリンタするとかチョロいですからね。
1、ラックが動く
歯車の材料は円柱です。
これにぎざぎざをつけます。
円柱にラックをグザグサ刺していけばいいらしいです。
どのくらいのペースでさすかっていうのは、ラックの並進速度とギアの基準ピッチ円の円周速度を一致させます。
で、台形のラックを動かすっておもえば
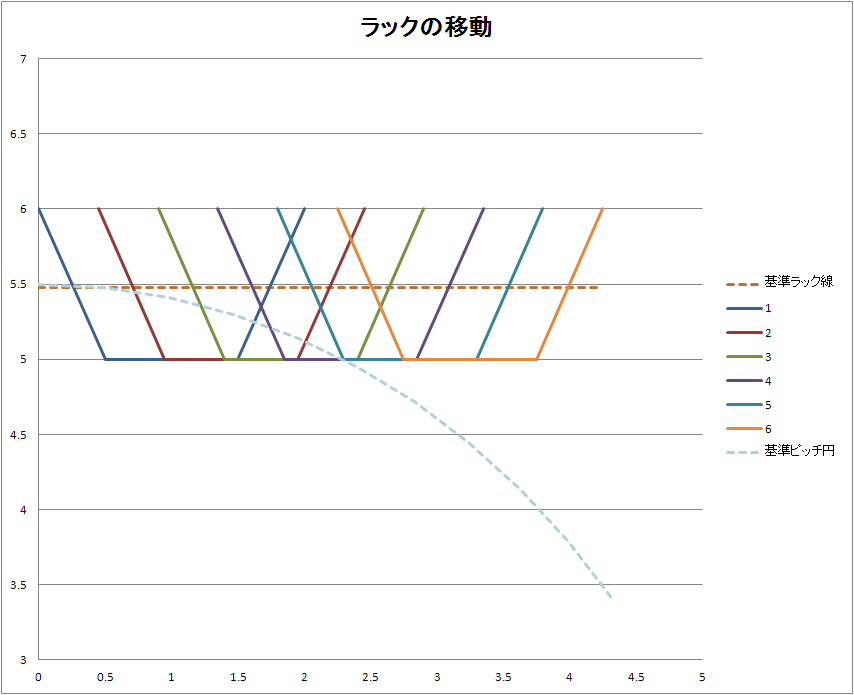 こんな感じです。
こんな感じです。
6ステップぐらい動かします。
ラックを移動→円柱を回転→加工ってなります。
台形の加工形状は円柱に付いて回ります。
加工形状はこんな感じになります。
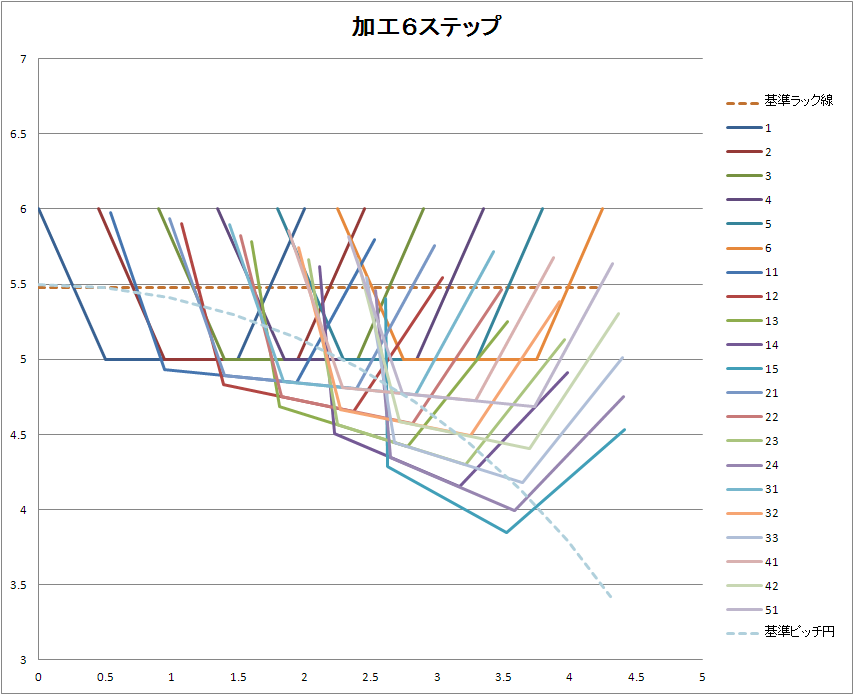 いっぱいになってよくわかりません。
いっぱいになってよくわかりません。
1ステップ目の加工形状は2ステップ目に回転します。
2ステップ目の加工形状は3ステップ目に回転します。
ステップが進むと加工形状がいっぱい重なります。
2、何度もラックがグサグサする
円柱に台形がぐさってなります。
で次のステップでは、前のステップの台形の加工形状に追加で加工がおこなわれます。
つまり2ステップ目は
ラックの移動と、加工の軌跡をかぶせた感じになります。
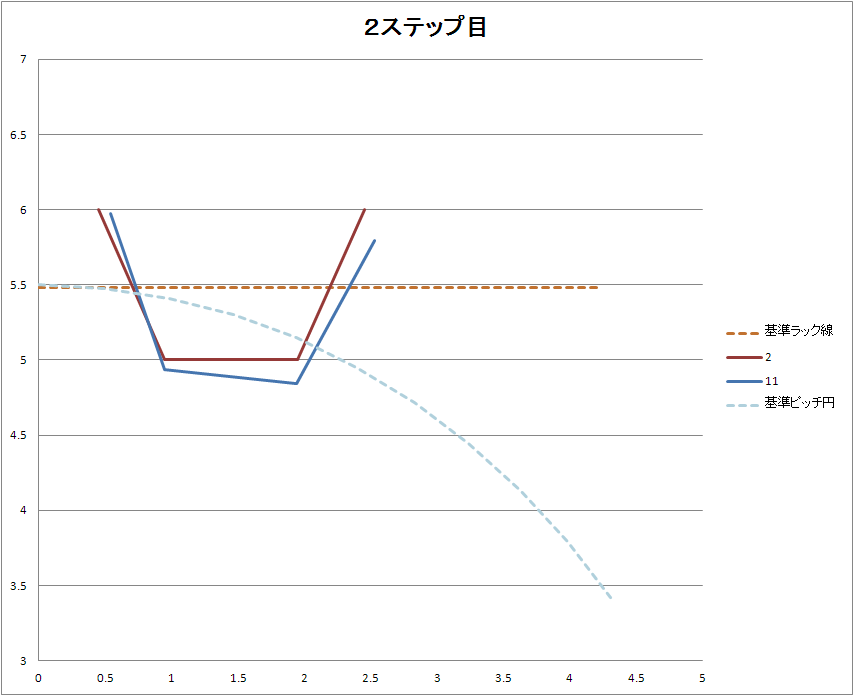 台形の穴に、ちょっとずらしてラックで削る感じですね。
台形の穴に、ちょっとずらしてラックで削る感じですね。
ちなみに3ステップ目は
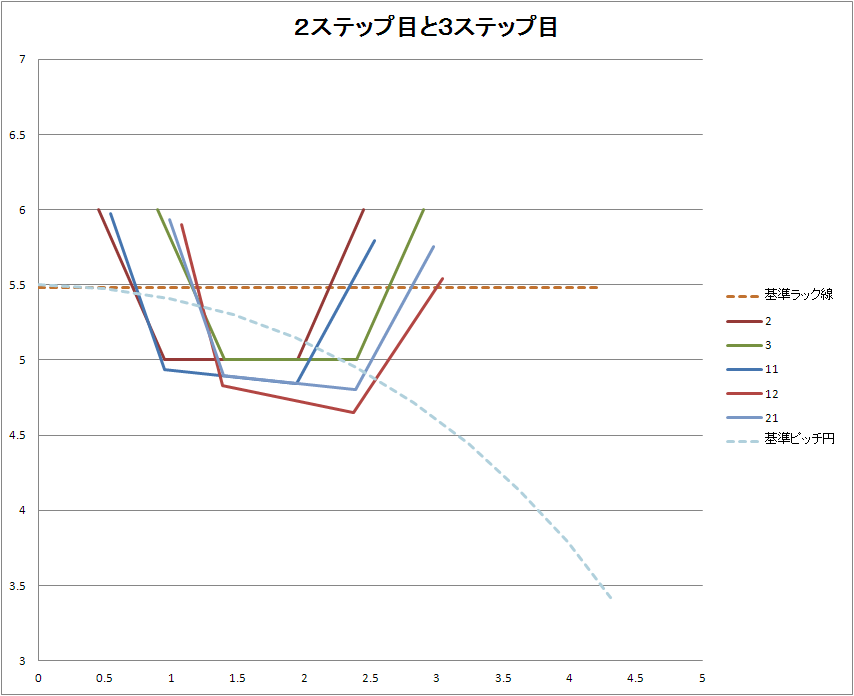 3つの台形を重ねた感じになります。
3つの台形を重ねた感じになります。
3、何回も繰り返すと歯形になる。。
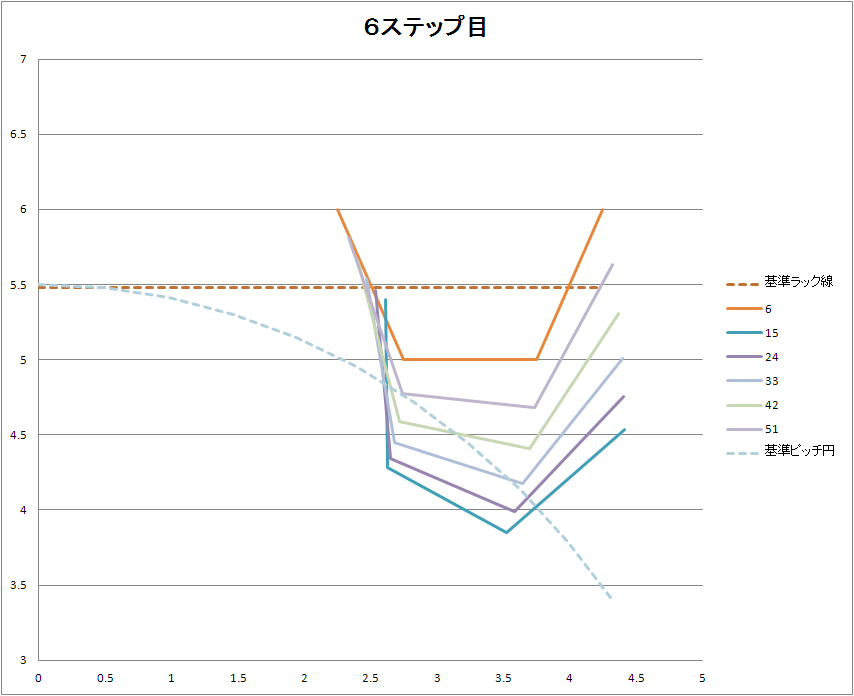 ラックの位置は右方向に6ステップ
ラックの位置は右方向に6ステップ
ギア材料の回転角度は時計回りに6ステップです。
6個の台形が重なります。
台形の左側面をみると歯形になってます。
あとは適当なスプラインでつなげればいいですね。
以上です。
これでみんな歯車が作れますね。おわり。
・そもそも歯の形状って何なの。
・インヴォリュートってなんなの。
・なんでうまくかみ合うの。
などなどいろんな不思議と戦う必要があります。
かなり世の中は不思議でいっぱいです。
ググってみると加工法は分かります。
ラックをつかうのとピニオンカッターをつかうのと・・・いろいろです。
というわけで、まずはどうやって歯形を得るかを考えてみます。
歯形が得られれば、NCで作るとか3Dプリンタするとかチョロいですからね。
1、ラックが動く
歯車の材料は円柱です。
これにぎざぎざをつけます。
円柱にラックをグザグサ刺していけばいいらしいです。
どのくらいのペースでさすかっていうのは、ラックの並進速度とギアの基準ピッチ円の円周速度を一致させます。
で、台形のラックを動かすっておもえば
6ステップぐらい動かします。
ラックを移動→円柱を回転→加工ってなります。
台形の加工形状は円柱に付いて回ります。
加工形状はこんな感じになります。
1ステップ目の加工形状は2ステップ目に回転します。
2ステップ目の加工形状は3ステップ目に回転します。
ステップが進むと加工形状がいっぱい重なります。
2、何度もラックがグサグサする
円柱に台形がぐさってなります。
で次のステップでは、前のステップの台形の加工形状に追加で加工がおこなわれます。
つまり2ステップ目は
ラックの移動と、加工の軌跡をかぶせた感じになります。
ちなみに3ステップ目は
3、何回も繰り返すと歯形になる。。
ギア材料の回転角度は時計回りに6ステップです。
6個の台形が重なります。
台形の左側面をみると歯形になってます。
あとは適当なスプラインでつなげればいいですね。
以上です。
これでみんな歯車が作れますね。おわり。
mbed備忘録7:KONDOシリアルサーボはじめました
ジャイロを買って、サーボも買って、mbedもかって・・・
シリアル用の回路つけてなんにもしてない日々が流れていたので、ちょっとあそびました。
◆まずはじめに、近藤の半2重通信をmbedにどうつなぐかです。
回路図はこんな感じ
mbedからの信号を5Vにしつつ半2重通信をします。
なぜそういうことをしようと思ったのか、それはもう思い出せません。
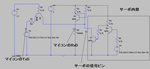
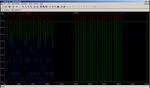
↑は赤がサーボのピン、緑がマイコンのRXD、青がマイコンのTXDそれぞれの電圧です。
マイコンから出た信号がマイコンに入っていますが、まー読まないから関係ないと思います??
ほんとかなぁ。
◆ほんでもって、ICS3.5をさーぼとやるので、シリアルをはいてやる必要があります。
コマンド方式サーボKRS-6003HVの制御 その1
こちらのプログラムを参考にさせていただきました。
また、本家のリファレンスも参考にしました。
ざっくり、こんな感じ
Serial ko(p9,p10);//txrx
void setServoDeg(float deg)//+-135deg
{
deg=deg+135;
if(deg>270)deg=270;
if(deg<0)deg=0;
targetPosi = 3500 + (int)((deg*800)/27);
}
//↑3500~11500で0~270°動きます。
float getServoDeg(void)
{
return (((float)(feedbackPosi-3500)*27)/800)-135;
}
/*----------------------------------*/
/* KONDOと角度 */
/*----------------------------------*/
int set_posi(char id, int pos)
{
unsigned char tx[3];
unsigned char rx[6];
int i;
int data=0;
tx[0] = 0x80 | id;
tx[1] = (unsigned char)( (pos >> 7) & 0x7f);
tx[2] = (unsigned char)(pos &0x7f);
for(i = 0; i<3; i++){
ko.putc(tx[i]);
}
//wait(16);
for(i = 0; i<6; i++){
rx[i] = ko.getc();
}
data = (int)(rx[4] & 0x7f);
data = (data << 7) + (int)(rx[5] & 0x7f);
return data;
}
int main(){
ko.baud(115200);
ko.format(8, Serial::Even, 1);
setServoDeg(もくひょうかくど);
feedbackPosi=set_posi(1, targetPosi);
↑それっぽいところだけ抜粋。
変数の宣言とか足りないと思う。
◆動かすだけじゃつまらないので、ジャイロとコラボしました。
カメラのジンバルっていうか、そんな感じの動画。
ジャイロの角速度"積分値"を、角度として入力すると、
回路の動いた角度だけ、サーボは逆転動作します。
つまり動いてないかのよう。
今回は5msごとにジャイロ取得、サーボに指令してます。
積分は何にも考えないで、
Σ(現在のジャイロ値×0.005)
です。
ジャイロは角速度を電圧にするんですけれでも、
ドリフトっていって動いてない時の電圧がだんだん増えていく弱点があります。
そこで、ハイパスフィルターとか淹れてみようって準備しました。
けど、動画の通りそこまで必要じゃなかったかっていう。
◆ハイパスフィルター
ゆっくりした変化を無視する方法がハイパスフィルターです。
こちらのプログラムを参考にしました。
簡単なデジタルフィルタの実装
ざっくりこんな感じで真似させていただきました。
// それぞれの変数は下記のとおりとする
// float samplerate … サンプリング周波数
// float freq … カットオフ周波数
// float q … フィルタのQ値
float omega,alpha,a0,a1,a2,b0,b1,b2;
float freq=.01;
float q=0.7071;
float samplerate=200;
/*----------------------------------*/
/* ハイパスフィルターセット */
/* Data入力 */
/*----------------------------------*/
void setHPF(void)
{
omega = 2.0 * 3.14159 * freq/samplerate;
alpha = sin(omega) / (2.0* q);
a0 = 1.0 + alpha;
a1 = -2.0 * cos(omega);
a2 = 1.0 - alpha;
b0 = (1.0 + cos(omega)) / 2.0;
b1 = -(1.0 + cos(omega));
b2 = (1.0 + cos(omega)) / 2.0;
}
float in1=0,in2=0,out1=0,out2=0;
/*----------------------------------*/
/* ハイパスフィルタ出力 */
/* Data入力 */
/*----------------------------------*/
float outHPF(float input)
{
// それぞれの変数は下記のとおりとする
// float input[] …入力信号の格納されたバッファ。
// flaot output[] …フィルタ処理した値を書き出す出力信号のバッファ。
// int size …入力信号・出力信号のバッファのサイズ。
// float in1, in2, out1, out2 …フィルタ計算用のバッファ変数。初期値は0。
// float a0, a1, a2, b0, b1, b2 …フィルタの係数。 別途算出する。
// 入力信号にフィルタを適用し、出力信号として書き出す。
float output;
output = b0/a0 * input + b1/a0 * in1 + b2/a0 * in2
- a1/a0 * out1 - a2/a0 * out2;
in2 = in1; // 2つ前の入力信号を更新
in1 = input; // 1つ前の入力信号を更新
out2 = out1; // 2つ前の出力信号を更新
out1 = output; // 1つ前の出力信号を更新
return out1;
}
ハイパスフィルターですから動画見たいに、動きが無くなる=高周波成分は0になろうとします。
普通はローパス分を別のセンサーとかを入れて相補するっぽいですが難しいことは・・・。
◆◆◆想像以上に積分値安定してるんで感動した。
シリアル用の回路つけてなんにもしてない日々が流れていたので、ちょっとあそびました。
◆まずはじめに、近藤の半2重通信をmbedにどうつなぐかです。
回路図はこんな感じ
mbedからの信号を5Vにしつつ半2重通信をします。
なぜそういうことをしようと思ったのか、それはもう思い出せません。
↑は赤がサーボのピン、緑がマイコンのRXD、青がマイコンのTXDそれぞれの電圧です。
マイコンから出た信号がマイコンに入っていますが、まー読まないから関係ないと思います??
ほんとかなぁ。
◆ほんでもって、ICS3.5をさーぼとやるので、シリアルをはいてやる必要があります。
コマンド方式サーボKRS-6003HVの制御 その1
こちらのプログラムを参考にさせていただきました。
また、本家のリファレンスも参考にしました。
ざっくり、こんな感じ
Serial ko(p9,p10);//txrx
void setServoDeg(float deg)//+-135deg
{
deg=deg+135;
if(deg>270)deg=270;
if(deg<0)deg=0;
targetPosi = 3500 + (int)((deg*800)/27);
}
//↑3500~11500で0~270°動きます。
float getServoDeg(void)
{
return (((float)(feedbackPosi-3500)*27)/800)-135;
}
/*----------------------------------*/
/* KONDOと角度 */
/*----------------------------------*/
int set_posi(char id, int pos)
{
unsigned char tx[3];
unsigned char rx[6];
int i;
int data=0;
tx[0] = 0x80 | id;
tx[1] = (unsigned char)( (pos >> 7) & 0x7f);
tx[2] = (unsigned char)(pos &0x7f);
for(i = 0; i<3; i++){
ko.putc(tx[i]);
}
//wait(16);
for(i = 0; i<6; i++){
rx[i] = ko.getc();
}
data = (int)(rx[4] & 0x7f);
data = (data << 7) + (int)(rx[5] & 0x7f);
return data;
}
int main(){
ko.baud(115200);
ko.format(8, Serial::Even, 1);
setServoDeg(もくひょうかくど);
feedbackPosi=set_posi(1, targetPosi);
↑それっぽいところだけ抜粋。
変数の宣言とか足りないと思う。
◆動かすだけじゃつまらないので、ジャイロとコラボしました。
カメラのジンバルっていうか、そんな感じの動画。
ジャイロの角速度"積分値"を、角度として入力すると、
回路の動いた角度だけ、サーボは逆転動作します。
つまり動いてないかのよう。
今回は5msごとにジャイロ取得、サーボに指令してます。
積分は何にも考えないで、
Σ(現在のジャイロ値×0.005)
です。
ジャイロは角速度を電圧にするんですけれでも、
ドリフトっていって動いてない時の電圧がだんだん増えていく弱点があります。
そこで、ハイパスフィルターとか淹れてみようって準備しました。
けど、動画の通りそこまで必要じゃなかったかっていう。
◆ハイパスフィルター
ゆっくりした変化を無視する方法がハイパスフィルターです。
こちらのプログラムを参考にしました。
簡単なデジタルフィルタの実装
ざっくりこんな感じで真似させていただきました。
// それぞれの変数は下記のとおりとする
// float samplerate … サンプリング周波数
// float freq … カットオフ周波数
// float q … フィルタのQ値
float omega,alpha,a0,a1,a2,b0,b1,b2;
float freq=.01;
float q=0.7071;
float samplerate=200;
/*----------------------------------*/
/* ハイパスフィルターセット */
/* Data入力 */
/*----------------------------------*/
void setHPF(void)
{
omega = 2.0 * 3.14159 * freq/samplerate;
alpha = sin(omega) / (2.0* q);
a0 = 1.0 + alpha;
a1 = -2.0 * cos(omega);
a2 = 1.0 - alpha;
b0 = (1.0 + cos(omega)) / 2.0;
b1 = -(1.0 + cos(omega));
b2 = (1.0 + cos(omega)) / 2.0;
}
float in1=0,in2=0,out1=0,out2=0;
/*----------------------------------*/
/* ハイパスフィルタ出力 */
/* Data入力 */
/*----------------------------------*/
float outHPF(float input)
{
// それぞれの変数は下記のとおりとする
// float input[] …入力信号の格納されたバッファ。
// flaot output[] …フィルタ処理した値を書き出す出力信号のバッファ。
// int size …入力信号・出力信号のバッファのサイズ。
// float in1, in2, out1, out2 …フィルタ計算用のバッファ変数。初期値は0。
// float a0, a1, a2, b0, b1, b2 …フィルタの係数。 別途算出する。
// 入力信号にフィルタを適用し、出力信号として書き出す。
float output;
output = b0/a0 * input + b1/a0 * in1 + b2/a0 * in2
- a1/a0 * out1 - a2/a0 * out2;
in2 = in1; // 2つ前の入力信号を更新
in1 = input; // 1つ前の入力信号を更新
out2 = out1; // 2つ前の出力信号を更新
out1 = output; // 1つ前の出力信号を更新
return out1;
}
ハイパスフィルターですから動画見たいに、動きが無くなる=高周波成分は0になろうとします。
普通はローパス分を別のセンサーとかを入れて相補するっぽいですが難しいことは・・・。
◆◆◆想像以上に積分値安定してるんで感動した。
4自由度ヘビの軌道生成?③
軌道上を通った場合の関節角度の決定方法は前回の通りです。
で軌道を決定する上での残ったパラメータは
●Sinの周期の長さ
●振幅
●↑とロボットのサイズ比
です。
こんかいは
2π:1:???
で???のところを、0.5,0.75,1.5(ロボットの3節を1:2:1とする)
というのを試しました。
で、ベターだったのは1.5です。
・・・ちなみに0.75では推進できませんでした。床にごむしーとを敷くと推進できましたが・・・つまり、摩擦が充分であればもっといい感じになるのでしょう。・・・広大なごむしーと・・・ほしぃ。
生成した軌道は
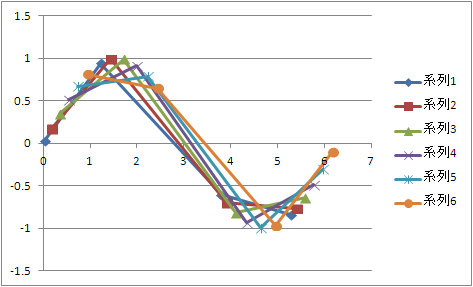
こんな軌道ととおり、
角度としては
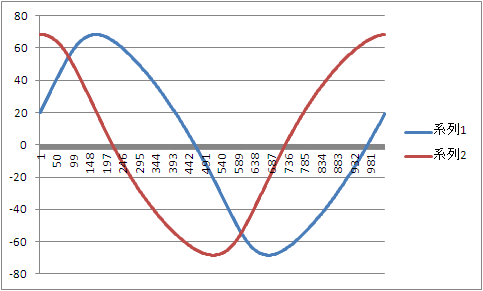
こんな感じになります。
後ろの関節と、前の関節の軌道は違うものでした。
「どっちが前?」というのは綺麗に分かれるようです。
実機の動作は
このようになり、前後というのははっきりしています。
動画からは、
・推進出来る時、出来ない時
・想定した軌道とのズレ
が明確に分かります。
なので、なるべく「推進できる時」というのを1周期ないで多く確保する軌道
というのを推定できると思いますが・・・
ま、あ、そろそろ飽きた・・・か・・・な。
で軌道を決定する上での残ったパラメータは
●Sinの周期の長さ
●振幅
●↑とロボットのサイズ比
です。
こんかいは
2π:1:???
で???のところを、0.5,0.75,1.5(ロボットの3節を1:2:1とする)
というのを試しました。
で、ベターだったのは1.5です。
・・・ちなみに0.75では推進できませんでした。床にごむしーとを敷くと推進できましたが・・・つまり、摩擦が充分であればもっといい感じになるのでしょう。・・・広大なごむしーと・・・ほしぃ。
生成した軌道は
こんな軌道ととおり、
角度としては
こんな感じになります。
後ろの関節と、前の関節の軌道は違うものでした。
「どっちが前?」というのは綺麗に分かれるようです。
実機の動作は
このようになり、前後というのははっきりしています。
動画からは、
・推進出来る時、出来ない時
・想定した軌道とのズレ
が明確に分かります。
なので、なるべく「推進できる時」というのを1周期ないで多く確保する軌道
というのを推定できると思いますが・・・
ま、あ、そろそろ飽きた・・・か・・・な。
プロフィール
HN:
Adel
年齢:
35
性別:
男性
誕生日:
1989/09/17
職業:
会社員
趣味:
モチベーション探し
自己紹介:
ロボットつくるのが夢
最新記事
(07/15)
(02/17)
(05/28)
(04/25)
(02/19)
カテゴリー
ブログ内検索
アクセス解析

