いろいろと｜明日の設計図

[PR]

×

[PR]上記の広告は3ヶ月以上新規記事投稿のないブログに表示されています。新しい記事を書く事で広告が消えます。

ソニーのSBH82Dという、オープンイヤーワイヤレスヘッドステレオヘッドセットを使うために苦労したのでブログにします。

PCはbluetooth内臓のthinkpadです。win7 SP1です。

○できない様子

・イヤホンをペアリングモードにする

・bluetoothデバイスの追加からSBH82Dを探して接続する

・ドライバのインストールが始まる

・ドライバが見つからない

使えない・・・

○できる様子
・BluetoothAudio ドライバなどとググる

・インテル@・・・・

・インストール用のexeをダウンロードする

・管理者実行する

・すごい時間がかかる

・サービスが停止できません、権限を確認云々がでる。

・bluetooth media service が停止できないとでる。

・msconfigから見ると停止中になっていて、そこからアクセスは何もできない

・インストールをキャンセルする

・PCを再起動する

・タスクマネージャのサービスから即刻、bluetooth media serviceを停止する

・インストーラを管理者実行する

・すごい時間がかかる→インストールできる

・イヤホンをペアリングモードにする

・デバイスの追加からSBH82Dを追加する

・ドライバのインストールが成功する

・デバイスサービスから接続する

・サウンドからBluetoothheadphonesが選べるようになる

・えらぶ

・適当に音を出す

[0回]

PR

有限角度のノンバックラッシプーリ伝達

簡単な部品でノンバックラッシ伝達ができないかと思ってチャレンジしました。
2本のテグス間にテンションをかけます。
小プーリで270deg動きます。

忘備録

回転の伝達なので、歯車かプーリかの２択です。
バックラッシのない歯車は超激レアなので重課金です。
タイミングベルトでプーリも面倒です。
ノンバックラッシにしようと思うと、いずれの場合も専門の加工が必要なので面倒です。

状況を有限角度に絞って簡単にすれば

・リンク

という選択肢があります。
が、リンクはノンバックラッシではありません。
重い部品が増えます。
構造物が増えることは作るのがめんどくさくなります。

結果として、リンクとプーリを組み合わせた感じにしました。

以下、こんな感じに作る。

２本のナイロンテグスをそこそこ同じ長さでつけて、
プーリを動かしてテンション調整して完成。

材料
3Dプリント部品４点
M3のねじが２本
6900ZZが４個
M2のねじが４本
ナイロンテグス適当

[1回]

実行ファイルにドラッグアンドドロップする。

忘備録

Cでテキストファイルを処理したいとき、アドレスのパスをどうやって渡すかいつも面倒だと思っていました。

で、よく考えると実行形式のファイルに乗っけて起動するタイプのソフトってありますよね。

だからそういうのできるんだと思ってググりました。

http://achapi2718.blogspot.jp/2012/06/c_1002.html

簡潔にまとめていただいているサイト様がありましたので記録しておきます。

後日、トライします。

[0回]

ルンゲクッタ法で微分方程式(単振動)を積分

創生×⇒創成○

だそうです。
大きな問題ですね。

シミュレーションに迫られておりまして、非線形微分方程式を積分したくなっております。

解析解は出ませんどころか、点群データなわけで。

シミュレーションに迫られています。

5年前にこのブログでもルンゲクッタ法にふれていましたが。
すっかり忘れたのでもう一度記事にします。

参考サイト様

簡単なシミュならオイラー法を使います。
dx/dt=Ax
であれば,刻みのステップをhとして
x1=x0+A*x0*h
という漸化式なので次々と計算すればいいです。
ただ、1次の傾きを積分していくので誤差が積もります。
そこで誤差の少ない方法が世間には広まっているのです。

その例としてルンゲクッタを選びました。
↑の式で進めると

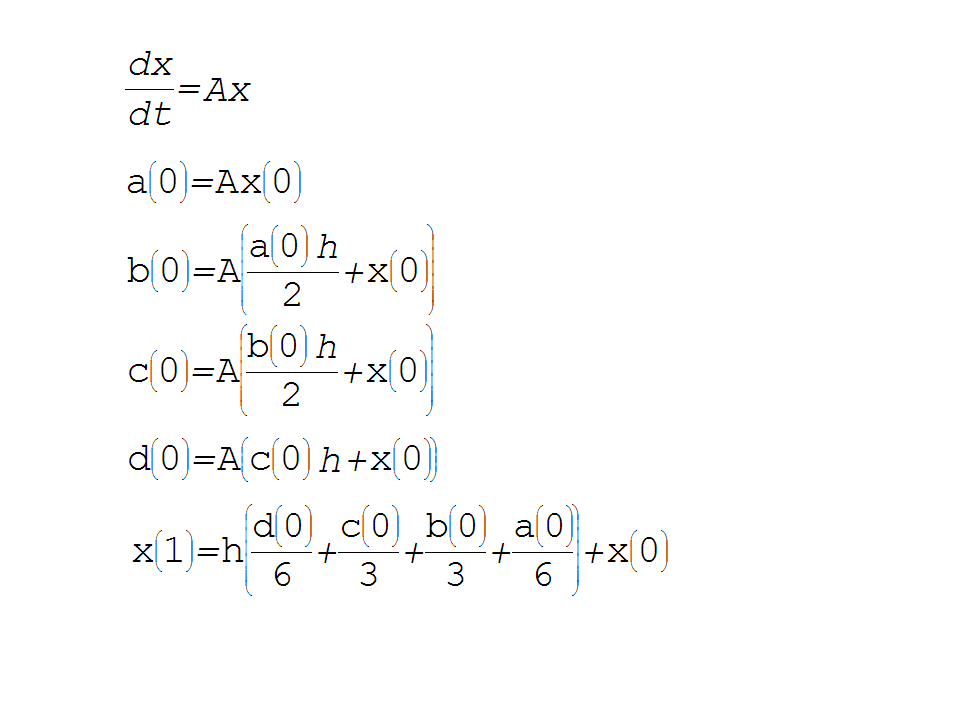a b c dという4つの係数から、理想的な傾きを求めるようです。
数値計算の教科書とかだと、一般的な常微分方程式を念頭に置いているので、単純な式だと返って分かりづらいものでした。
引数？がだいぶ減るので簡単です。
例えば、
dx/dt=A*t*x
みたいな場合であれば、もう少し教科書寄りの式に成ります。

で、どのくらい精度がいいかということですが

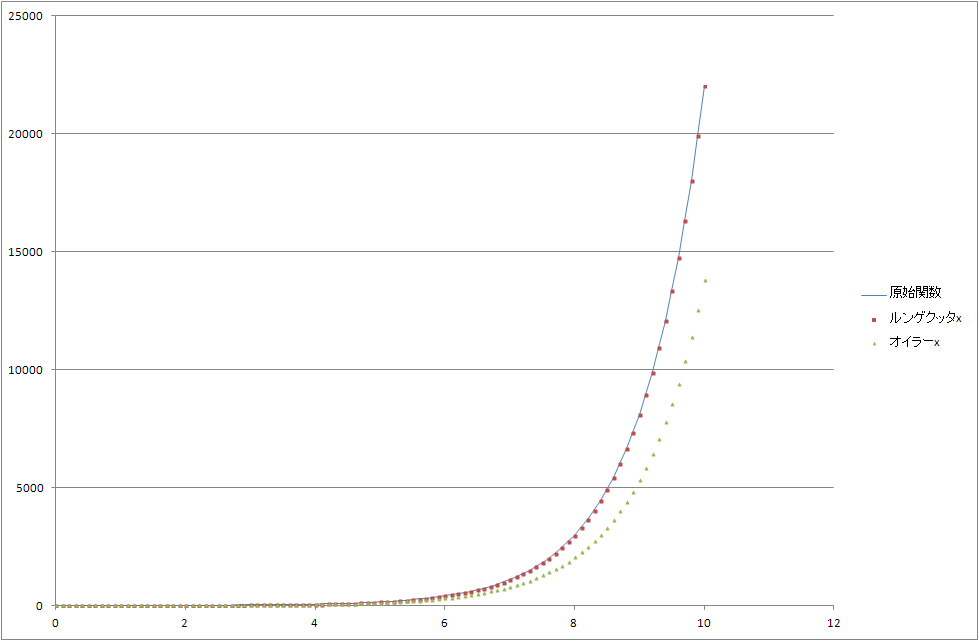
ただのexpカーブが解析解となりますが、このようにオイラーだと離れていくところが付いていくわけです。

でもって、簡単なところはこの辺で。

もう少し応用の利く例を置いておきます。
運動方程式であれば、2階の微分方程式だと思います。
d^2x/dt^2=Bx
みたいな。
Bが負であれば単振動です。

計算は、状態方程式のように2つに分けて、y1,y2の連立の１階微分方程式にします。

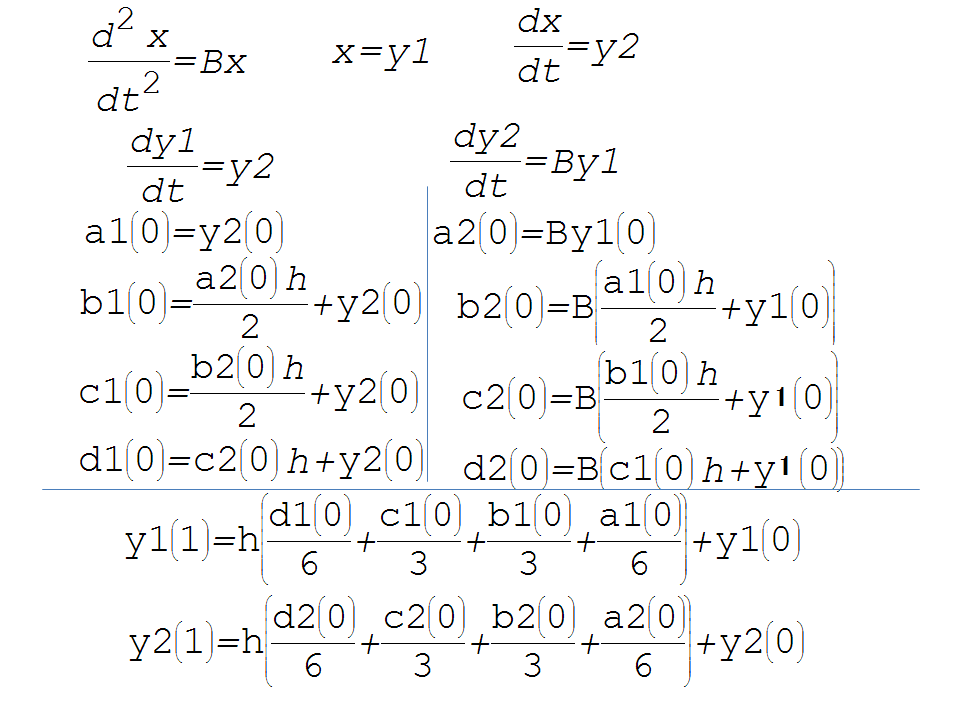
さっきと同様にa b c d を計算しますが、
y1とy2の流れを交互にやることに注意します。
y2のb、つまりb2はa1を使って計算する必要があります。
少し複雑です。

計算結果です。

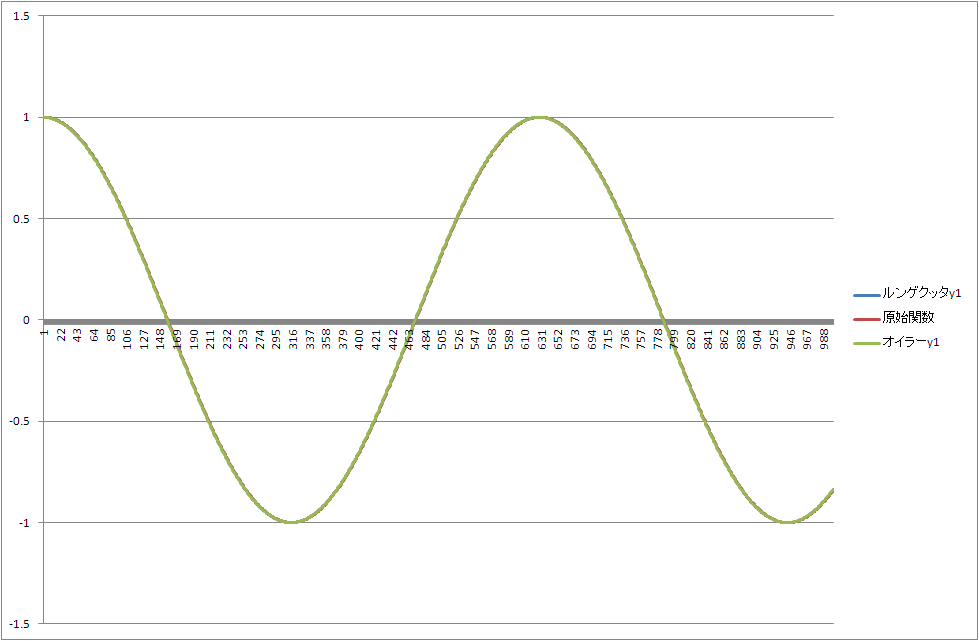B=-1だと思いますが。
ざっくりこんな状態です。

オイラーでもほとんど一緒です。
ですが、解析解との差分をみると

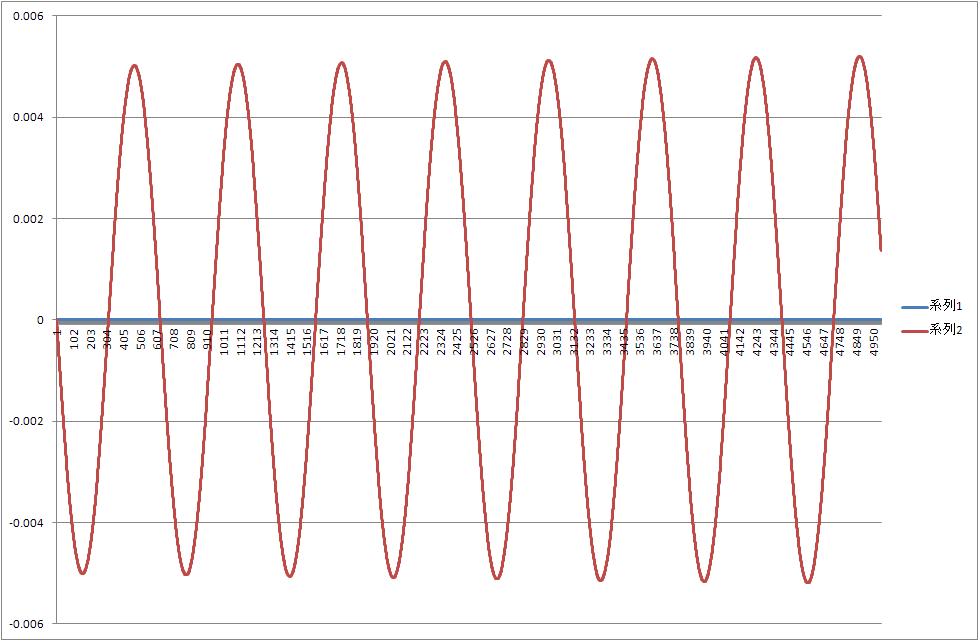このようになっているので、ルンゲクッタの頑張りようがわかるのではないでしょうか。

ダウンロード

元エクセルを置いておきます。内容は整理していませんのですいません。

さて、２階だろうが、連立だろうができるようになりましたので、
多質点の運動方程式に手が届きます。

それはまた今度。

[0回]

歯車創生2

歯車どうやって作るシリーズ再開です。

ぜんかい、図形を少しずつずらしていくと曲線が見えてくる⇒これが歯だ

という展開でしたが、ではその曲線そのものはどんな関数としてあらわされるのか？

で、ネットサーフィンの果てに"包絡線"というものを見つけました。

参考サイト様http://hooktail.sub.jp/mathInPhys/envelope/

直線をずらしていく
線が一杯引ける
さて、その線群はどんな曲線を描くか？

現在の理解レベル：
①曲線に一つ変数を加えて、ずらすことを表現する　←　歯車は１自由度だから当然か…
②その曲線群関数を加えた変数で偏微分する
③連立させて変数を消す
④勝利

・・・☆

というのは難しいので、既にある曲線から接線の群を取り出し、曲線を見いだすという実験をしてみます。
２次関数は

てなかんじで接線の方程式がもとめられますね！

接線を一杯描いてみる＆２次関数と重ねる

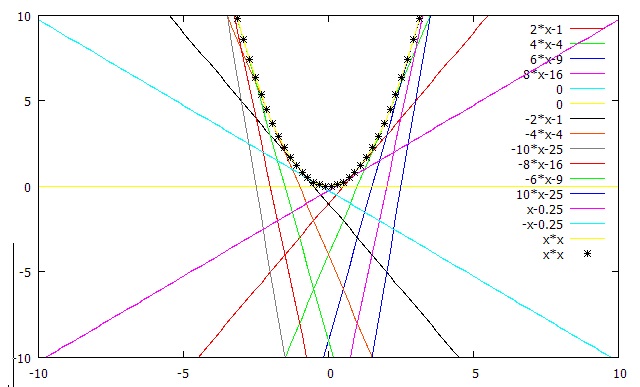
JPEGで張り付けるとカスみたいな画質ですね。
ちなみにθを0.5:5まで正負いれてみた接線と、
２次関数は分かりづらかったのでアスタリスクで出しました。
間違えた線も入ってますけど、
まーこんなかんじっていうイメージを掴むには充分と思います。

では、やってみますか
①曲線に一つ変数を加えて、ずらすことを表現する　←　歯車は１自由度だから当然か…
②その曲線群関数を加えた変数で偏微分する
③連立させて変数を消す
④勝利

勝利しましたね。
世の中大したことありません。

はて、接線群の関数の偏微分とはどういう意味でしょうか？
偏導関数なので、接した時の向きを言っています。
で、それは(x,y,θ)を通ると言っているのです。

・・・よくわかりません。偏微分を勉強しましょう。

[0回]

歯車創生１

★ロボットを作っていくうえでギアが必要ですが、ギアはどうやって作るんでしょう？

・そもそも歯の形状って何なの。
・インヴォリュートってなんなの。
・なんでうまくかみ合うの。

などなどいろんな不思議と戦う必要があります。
かなり世の中は不思議でいっぱいです。

ググってみると加工法は分かります。
ラックをつかうのとピニオンカッターをつかうのと・・・いろいろです。
というわけで、まずはどうやって歯形を得るかを考えてみます。

歯形が得られれば、NCで作るとか3Dプリンタするとかチョロいですからね。

１、ラックが動く
歯車の材料は円柱です。
これにぎざぎざをつけます。

円柱にラックをグザグサ刺していけばいいらしいです。
どのくらいのペースでさすかっていうのは、ラックの並進速度とギアの基準ピッチ円の円周速度を一致させます。

で、台形のラックを動かすっておもえば

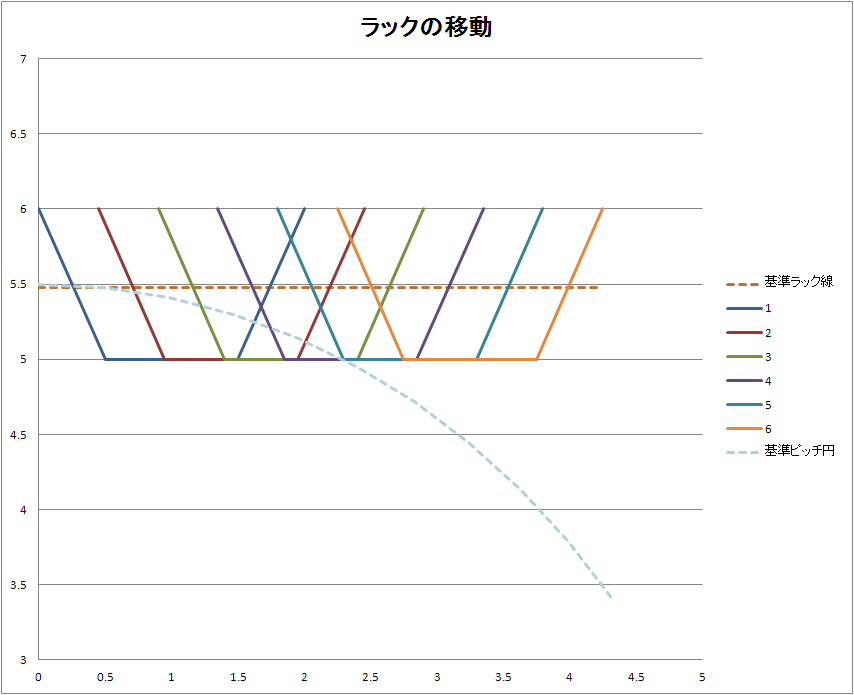こんな感じです。
６ステップぐらい動かします。
ラックを移動→円柱を回転→加工ってなります。
台形の加工形状は円柱に付いて回ります。
加工形状はこんな感じになります。

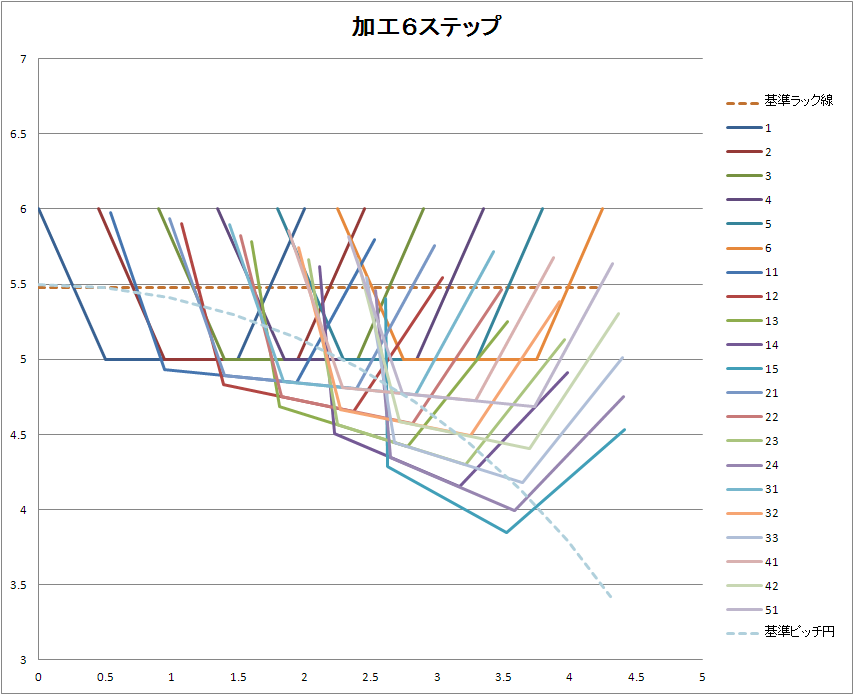いっぱいになってよくわかりません。
１ステップ目の加工形状は２ステップ目に回転します。
２ステップ目の加工形状は３ステップ目に回転します。
ステップが進むと加工形状がいっぱい重なります。

２、何度もラックがグサグサする
円柱に台形がぐさってなります。
で次のステップでは、前のステップの台形の加工形状に追加で加工がおこなわれます。
つまり２ステップ目は
ラックの移動と、加工の軌跡をかぶせた感じになります。

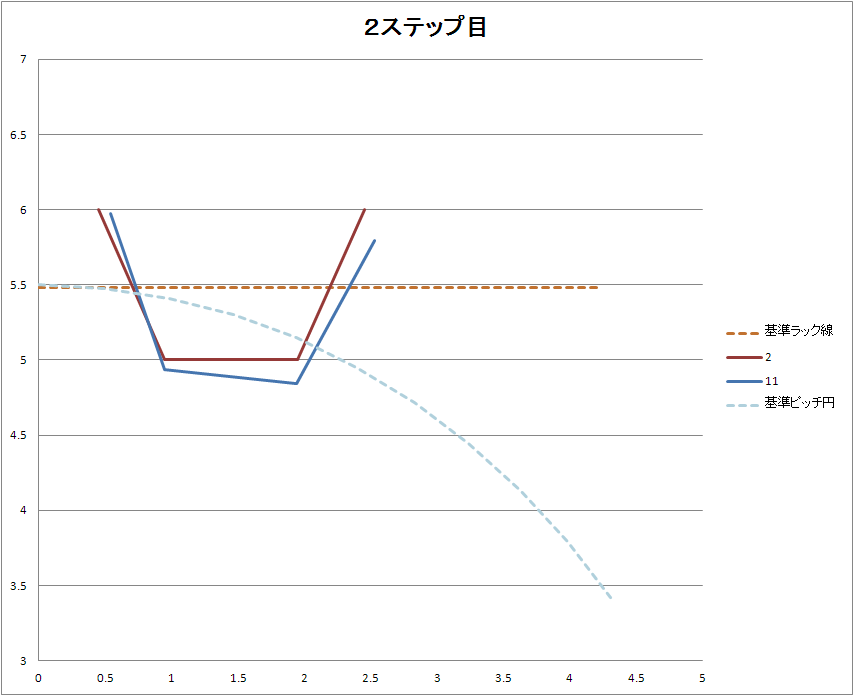台形の穴に、ちょっとずらしてラックで削る感じですね。

ちなみに３ステップ目は

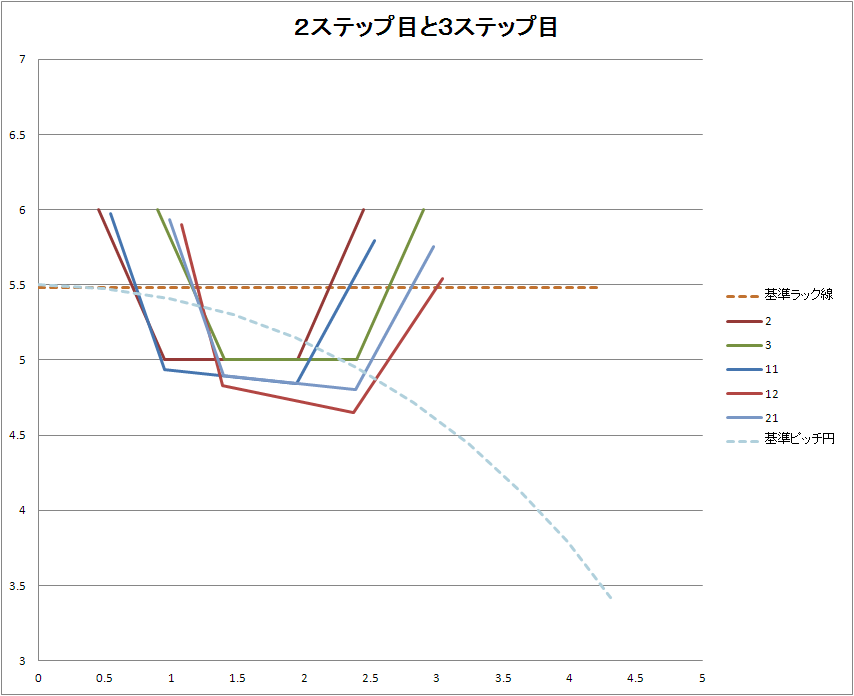３つの台形を重ねた感じになります。

３、何回も繰り返すと歯形になる。。

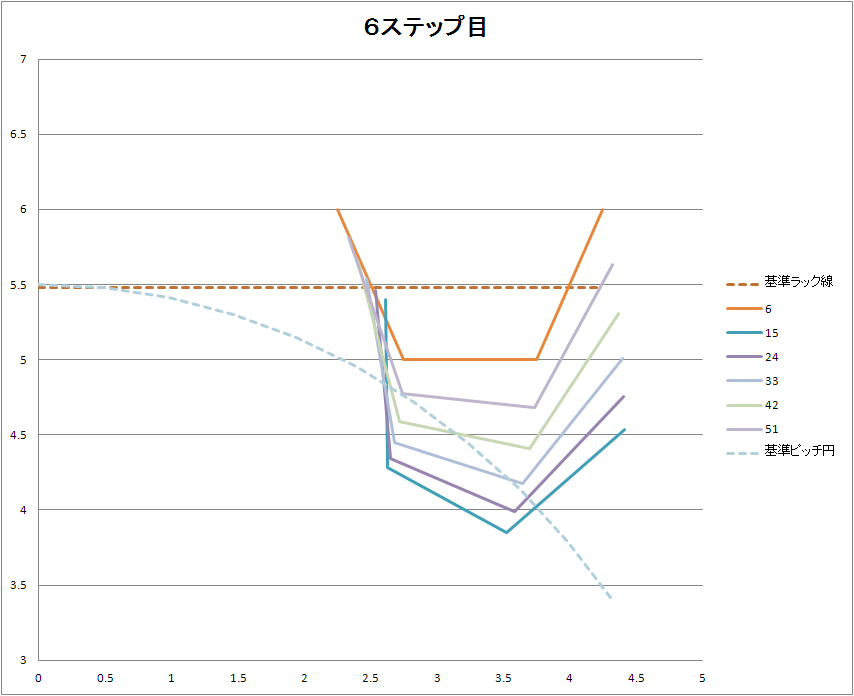ラックの位置は右方向に６ステップ
ギア材料の回転角度は時計回りに６ステップです。
６個の台形が重なります。
台形の左側面をみると歯形になってます。
あとは適当なスプラインでつなげればいいですね。

以上です。
これでみんな歯車が作れますね。おわり。

[1回]

アクリルの加工依頼

ブログの更新が無いのは、ロボロボしてないからです。

ロボロボしたわけではないですが、人柱的な備忘録的なものです。

本日紹介するのはこれ

アクリルの円筒です。
Φ14.8h8のRa12.5を指示して加工依頼をだしました。
５０個頼んで￥15,000弱でした。

個人で削りの加工依頼をするのはなかなか難しいものです。

図面送る→見積もらう→加工方法など相談→再見積→注文
という流れが一般的かと思います。

しかし、加工屋さんによってはそもそも個人相手をしてくれなかったり、対応が遅かったり、まー思った通りにはいきません。

そんなわけで今回、思い通りのものをササッとやってくれたお店を紹介です。

アクリ屋ドットコムさんです。
http://www.acry-ya.com/

もともと、定尺の板だけでなく寸法を指定してWeb上で見積も出してくれる便利なところです。
凄いのは穴加工とかもWeb上で指示できるし、見積もでる。

という凄いところですが、今回はまず、
「このくらいのサイズのものが欲しいんですけど、図面とか送ったらやってくれますか？」
っていう趣旨のメールを出しました。

そしたら、やってくれました。図面を送って見積書をもらいました。
しかもその見積書はWebページと連動してまして・・・カートに入れるとか、そういう感じで注文が出来たし、クレジットで払いました。

いやはや、アパート暮らしになってお家で旋盤なんてちょっとと思いましたが、
値段は高く付きますが、これはありだなと思います。

[0回]

wxMaximaにて列ベクトルの外積：備忘録

いろいろとあって、逆運動学するソフトがひつようになりました。
そこでフリーソフトのmaximaをチョイス！

いろいろをまず解説すると、
６軸マニの逆運動学を行う、、、には
ヤコビアンで数値計算がひつようぽい、、、ので
同次変換行列を計算して、、、
６軸分のヤコビアンを求める、、、となり
関節ごとの同次変換行列から、回転軸の単位ベクトルと関節位置を使いヤコビアンを求める、、、つまり
回転軸が分かって角速度を与えれば、後は腕のながさで次の関節の位置の速度と角速度が出ると、、、そういうわけで

腕の長さベクトルと回転軸周りの角速度ベクトルを外積しないといけません！

つまり同次変換行列から、列ベクトルを抜き出して外積してその結果から新たにヤコビアンの行列を生成します。

で、maximaには標準で外積の機能がりません←どうしてこうなってる？

調べるとべクトル用のパッケージがあってそれを使えばできるとかなんとか・・・

load(vect);

u:[a,b,c];

v:[x1,x2,x3];

express(u~v);

って書くとこうなる↓
[b*x3-c*x2,c*x1-a*x3,a*x2-b*x1]

いいじゃんねー。

だがしかし、これは行ベクトルというより、単なるリストなのです。

ちなみに1行しかないmatrixで宣言すると

load(vect);

u:matrix([a,b,c]);

v:matrix([x1,x2,x3]);

express(u~v);

って書くとこうなる↓
~ used with improper arguments: matrix([a,b,c])matrix([x1,x2,x3])
#0: express1(expn=matrix([a,b,c]) ~ matrix([x1,x2,x3]))(vect.mac line 166)
-- an error. To debug this try: debugmode(true);

くそだ、なんだこれ

そんなわけで、関数を定義します。

cros(a,x):=matrix(a[2]*x[3]-a[3]*x[2],a[3]*x[1]-a[1]*x[3],a[1]*x[2]-a[2]*x[1]);
コレ、テストに出ル。

結果

あ、間違ってる、画像治すのめんどいけどプログラムはなおす。
u1v3-u3v2×
u2v3-u3v2○

はい、できました。

寝ましょう。

[1回]

ガタガタとCut3DとMeshCAM

CAMを用いてSTLデータからNCコードを生成しCNCフライスで加工するときに思ったことをつらつらと書きます。
CADCAMについて、何か専門的に勉強したことがあったり、何らかの科目で説明を受けたりということは一切ないので、ネーットサーフィンと実際にやってみた！事実をもとに考えてみたことなので、ある意味常識てきなこと、あるいは非常識なことを多分に含んでいるし、内容が他大多数の人と共有できる物なのかどうかということには

全く興味が無い

ですが、自分の備忘録としてまとめたものです。

機材：
miniCNC-HAKU MACH3
エンドミルはミスミの１０DロングエンドミルΦ2
切り込み量0,2mm
x-y送り600mm/min
z送り100mm/min
主軸（設定上8000rpm）

CAMソフト：
Cut3D(http://www.originalmind.co.jp/goods/03518)
MeshCAM(http://www.originalmind.co.jp/goods/03516)

アジェンダ
■Cut3Dで部品がガタガタに削れた！
■STLの解像度って何だ？
■解像度を変えて加工してみる！
■MeshCAMってなに？
■切削時間とNCコード生成とやる気

◇そもそも

こんな感じの部品
材質ABS
高さ10mm
150x150ぐらいのサイズ。

与えられている材料
厚み10.8mmの板

やりたい加工
0.8mm表面を削る
2次元パスを削る

◇結論
Cut3Dは微妙。MeshCAMはまーゆるせる。

◇ガタガタ
今回削ったものを右から順に並べます。

右から①②③④⑤の加工とします。

まず①を加工しました。
斜めのところ、Rのところがガタガタです。
は？と思います。
軸がぶれぶれとか、メカ的なバックラッシュとか・・・かな？
と思いました。
ですが、②の時は加工の一部始終を見ていましたがそんな感じはしないし、
実際にメカをオラオラってゆすってみてもバックラッシュはないかな？
少なくともこんなにガタガタは感じないし。
そもそも斜めの面に出てる時点でx-y軸いずれもバックラッシュがあると仮定すると、
他のまっすぐパスのx移動からy移動に変わった時に後ができるハズだし・・・
（これって円が削れないよね…）

ソフトてきな？

はいはい、では加工の流れでソフトが絡む部分を考えます。

3DCAD作る⇒STLで保存⇒CAMソフトで読み込み⇒切削パラメータ入れて⇒NCコード生成
少しネットサーフィンして、STLが有限要素法みたいに３角形にするものだと知った。
つまり？細かい直線がいっぱいで曲線を表すっぽい。

へ？曲線

斜めって直線だし…。
は？は？

じゃあ、NCパスを眺めてみるか
NCviewerなるものをグーグル先生に教えてもらい
つかう。

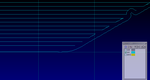
横の平行ラインは0.8mmの削りです。←まーどーでもいい。
問題は横線とRと斜め線の部分。
よーく見るとガタガタである。

つまりNCコードはガタガタ、メカは正常に動いている！！

敵は何処や？
Cut3Dのパラメータとか？
STLデータの解像度とか？

Cut3Dの設定をなめまわす。
それっぽい設定はなんにもない。

じゃあSTLの解像度的な？

STLの保存の際の設定を見る。

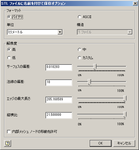
おっと割といろんな設定があった←しらなかった…。

これかも！！

（ぬかよろ。）

で、設定をいろいろ変えてみた。
で上の②③④の加工順に解像度を上げたわけです。

写真をみるとおり、みんなガタガタ、ガタガタの様子が少し筒違いますが・・・
まー、振幅の大きさは変わらないというか・・・

STLの解像度ではなかった！

CADの寸法精度的な

そんなバナナ。（Cut3D以前に2DのＣＡＭでは何べんもやってみて問題なかった経験大アリ）

ではCut3Dの設定or仕様

そこで来たのが、別の3DCAMを使ってみる。
辛辣な後輩から提案されたのはMeshCAM...
説明を読むと製作元が違う

・安い
・仕上げパスの種類が多い
・フリーフォー１５日

ふむふむやってみる。

試行錯誤の後同じような部品が作れると思われるパスを生成。
Cut3Dとはチト趣が違う。簡単に言えば
◇Cut3D⇒２種一括パス（0.8までジオメトリの形状オフセット刃径含む、に表面を削る）＋（ジオメトリの形状に合わせ一番下まで、0.2ずつ等高パス）

◇MeshCAM⇒２種別パス・・・設定を変えて２度パスを生成する。
１、表面を削る…これが難しい。ジオメトリ形状まではできる、問題は刃径オフセット付けると10.8まで削ろうとする。表面だけじゃなくて溝に手を出し始める。
２、等高パス…これはちょっと難しい。材料設定を10.8にしても、部品が10mmだと野郎は（仕上げパスだし…）と思っているのか10mmから削り始める。

※気付いたかもしれないが、オフセット無しの表面削りと、10mmからの等高パスを連続でやると…等高パスはジオメトリ形状の外側をエンドミルが通るわけで・・・一回めの切り込みが10.8ある部品に0.8以上一気に切り込むことになります。
まー樹脂ならいいかもですが、アルミとかはとても無理かと思います。
実際は刃径の7割ぐらいオフセットして表面削りパスを作ることで緩和できますが…緩和しかできません。

俺は気付いた！！

表面削りの時の材料の厚みを0.8しかないことにすればよくね！！
10mmからしかジオメトリが無いので、ジオメトリ形状が選べません…
なので0.8＋一回分の切り込み量ぐらいの材料サイズにするのが正解か？

というわけで

写真一番左の綺麗な面の加工が完了しました。
一個目の加工が終わってから、もう一回データ入力して2個目の加工ってなるので手間ですね。

◇この手間を持ってすれば、削れます。一発でやりたい人はガタガタに成るでしょう…。
俺は1発でやりたかったんですが…
今のところムリです。

おわり

[5回]

PSE9で自作アイコン

デスクトップにひしめくアイコン達。

このなかでもキラリとひかる逸材とかがいれば、すぐに見つけられる。

ショートカットとか見つけられない。

だって、ただのフォルダに小さい矢印付いただけじゃん…。

というわけで、自作アイコンでショートカットをわかりやすく表示したいと思った次第。

で、アイコン作成は拡張子いじっただけとかではできないみたいでした。

せっかく3ｋぐらいPSE９かったわけですので、使いたいきんめだい。

ですがPSEでもすぐはできない。

んで、
http://d-skate.xsrv.jp/2008/05/photoshopico.html
http://dropwne.jugem.jp/?eid=372
こちらのサイトを参考にさせていただきました。

んで、
いろいろやると保存するときの形式にICOが出現します。

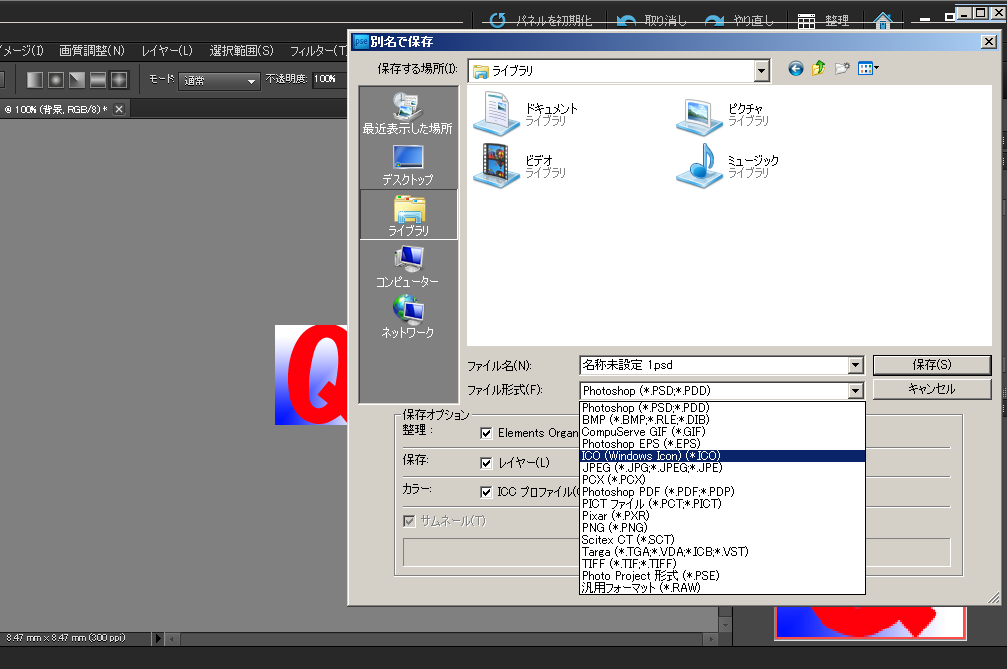
んで、
ショートカットアイコンを右クリックして、プロパティからアイコンを変更します。

アイコンはサイズとかなんとかいろいろあるみたいだけど、よく知りません。
でもアイコン作れたからいいや。

おわり。

[0回]