最近面白い話がないので更新することがないので、なんかして持論を展開する。
～軸受け径に大小がある場合のガタの変化とその利用～
1、はじめに
ベアリングを用いた軸受には、一つのベアリングを利用したものと、2つのベアリングを利用したものがある。特に、1つの軸受の場合片持ちなどと言ったりして、ガタが大きくなったりする。それに対し、2つのベアリングを距離を置いて一つの軸に利用することで、大幅にガタを減らすことができる。本稿は後者の2つのベアリングを利用する際、軸径を変化させた場合を想定する。
2、軸のガタのモデル化とパラメータ
図１に次のような軸の配置を考える。
[fig.1左：同径軸受、右：異径軸受]
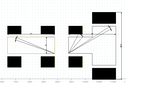軸受の距離、すなわち左右の距離は同じとする。そして、図1のように軸と軸受に微小な隙間を想定し、接触までの角度を考える。
この時、特に右の図のようなときの回転中心で、大径の接触角度をグラフに表す。
接触角度Θは、軸径を（ｄ１、ｄ２）、隙間を（ｌ）、図のおける軸の両端距離を（D）とすると
Θ＝asin[ { ( (d1+d2)/2) + l } / { sqrt( ( (d1+d2)/2 )^2+D^2 ) } ]
- asin[ { (d1+d2)/2 } / { sqrt( ( (d1+d2)/2 )^2+D^2 ) } ]
のようになる。この時ｄ１を固定し、ｄ２をｄ１の半分から、1.5倍に変化させた結果が図2となる。
[fig.2]
これによれば、小さくなればなるほど減り、大きくなればなるほど、増す。すなわち、大小どちらを回転中心とするかによって大きく変化することが分かる。
3、結論
本稿は、2重軸受の径の大小によるガタの変化について幾何学的に2次元解析し、議論した。大小2種の軸受を利用することにより場合によっては、同径の軸受を二つ用意するよりもガタを減らすことが分かった。しかしながら、同時にガタを大きくする恐れがあることもわかった。これについては、周りのフレームの形状によって変化するのでさらに周辺形状もモデル化し、解析する必要がある。だが既に形状が完成している際の設計確認などの際は本稿が参考になるのではないかと思う。
ふ～ん。よくわからないな。
で、どうしろと？
さぁ。寝よう。
[0回]
PR
